Persamaan kuadrat, persamaan polinomial derajat dua, merupakan landasan penting dalam aljabar dan matematika yang lebih tinggi. Pemfaktoran, teknik memecah persamaan kuadrat menjadi faktor-faktor linearnya, sangat penting untuk memahami dan menyelesaikan berbagai masalah matematika dan sains.
Dalam uraian ini, kita akan mengeksplorasi konsep persamaan kuadrat, metode pemfaktoran, jenis-jenis persamaan kuadrat, dan aplikasinya dalam kehidupan nyata. Dengan pemahaman yang mendalam tentang pemfaktoran persamaan kuadrat, kita dapat membuka kunci berbagai solusi masalah yang menantang.
Konsep Persamaan Kuadrat

Persamaan kuadrat adalah persamaan polinomial yang memiliki derajat kedua. Bentuk umumnya adalah ax² + bx + c = 0, di mana a, b, dan c adalah konstanta real dan a tidak sama dengan 0.
Contoh persamaan kuadrat:
- x²
– 5x + 6 = 0 - 2x² + 3x
– 5 = 0 - -x² + 4x
– 3 = 0
Variabel dalam persamaan kuadrat adalah x, sedangkan a, b, dan c adalah konstanta.
Pemfaktoran Persamaan Kuadrat
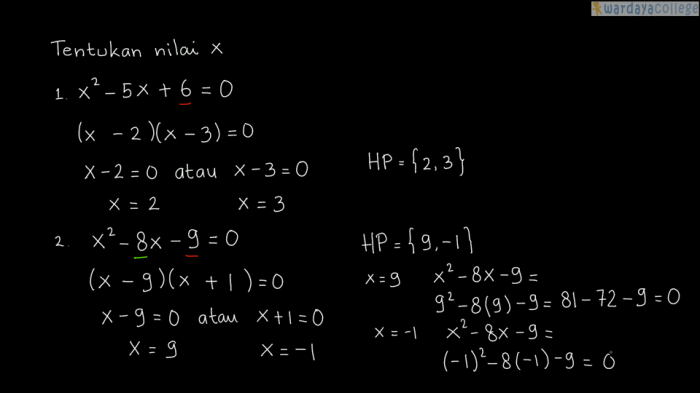
Pemfaktoran persamaan kuadrat adalah proses penguraian persamaan menjadi bentuk perkalian dari dua atau lebih faktor linear.
Langkah-langkah umum pemfaktoran persamaan kuadrat:
- Tuliskan persamaan dalam bentuk standar (ax² + bx + c = 0).
- Temukan dua bilangan yang jumlahnya sama dengan b dan hasil kalinya sama dengan ac.
- Tulis ulang suku tengah (bx) menggunakan bilangan yang ditemukan pada langkah 2.
- Faktorkan menggunakan pengelompokan.
- Sederhanakan faktor-faktornya.
Metode Pemfaktoran
| Metode | Kondisi | Contoh |
|---|---|---|
| Pemfaktoran Selisih Kuadrat | a = 1 dan b ganjil | x²
|
| Pemfaktoran Jumlah Kuadrat | a = 1 dan b genap | x² + 6x + 9 = (x + 3)² |
| Pemfaktoran Perbedaan Kuadrat | a > 1 | 4x²
|
| Pemfaktoran Trinomial Sempurna | a = 1 dan b dan c adalah kuadrat sempurna | x² + 2xy + y² = (x + y)² |
| Pemfaktoran Trinomial Umum | Tidak ada kondisi khusus | x²
|
Contoh Pemfaktoran Persamaan Kuadrat
Contoh 1: Pemfaktoran Selisih Kuadrat
x² – 9 = (x + 3)(x – 3)
Contoh 2: Pemfaktoran Perbedaan Kuadrat
4x² – 25 = (2x + 5)(2x – 5)
Contoh 3: Pemfaktoran Trinomial Umum
x² – 5x + 6 = (x – 2)(x – 3)
Jenis-Jenis Persamaan Kuadrat
Persamaan kuadrat dapat diklasifikasikan menjadi beberapa jenis berdasarkan jumlah dan sifat akarnya.
Berdasarkan Jumlah Akar
- Persamaan Kuadrat yang Memiliki Dua Akar Real dan Berbeda
Persamaan kuadrat ini memiliki dua akar real yang berbeda, yang dapat positif, negatif, atau nol. Misalnya: x²
– 5x + 6 = 0. - Persamaan Kuadrat yang Memiliki Satu Akar Real Berlipat
Persamaan kuadrat ini memiliki dua akar real yang sama, yang dapat positif, negatif, atau nol. Misalnya: x²
– 4x + 4 = 0. - Persamaan Kuadrat yang Tidak Memiliki Akar Real
Persamaan kuadrat ini tidak memiliki akar real dan memiliki dua akar kompleks konjugat. Misalnya: x² + 2x + 5 = 0.
Berdasarkan Sifat Akar
- Persamaan Kuadrat yang Memiliki Akar Rasional
Akar-akar persamaan kuadrat ini dapat dinyatakan dalam bentuk pecahan atau bilangan bulat. Misalnya: x²
– 5x + 6 = 0. - Persamaan Kuadrat yang Memiliki Akar Irasional
Akar-akar persamaan kuadrat ini tidak dapat dinyatakan dalam bentuk pecahan atau bilangan bulat, melainkan dalam bentuk akar kuadrat. Misalnya: x²
– 2x + 2 = 0. - Persamaan Kuadrat yang Memiliki Akar Kompleks
Akar-akar persamaan kuadrat ini adalah bilangan kompleks, yaitu bilangan yang memiliki bagian real dan imajiner. Misalnya: x² + 2x + 5 = 0.
Aplikasi Pemfaktoran Persamaan Kuadrat

Pemfaktoran persamaan kuadrat memiliki berbagai penerapan dalam kehidupan nyata, terutama dalam bidang matematika dan fisika.
Pemfaktoran persamaan kuadrat memungkinkan kita untuk memecahkan persamaan tersebut menjadi faktor-faktor yang lebih sederhana, sehingga memudahkan kita untuk menemukan solusi atau akarnya.
Aplikasi dalam Matematika
- Menyelesaikan persamaan kuadrat dengan mudah dan cepat.
- Mencari nilai maksimum atau minimum fungsi kuadrat.
- Membuat grafik fungsi kuadrat.
Aplikasi dalam Fisika
- Menghitung lintasan suatu benda yang bergerak dengan percepatan konstan (gerak parabola).
- Menentukan kecepatan benda yang dilempar vertikal ke atas.
- Menghitung ketinggian maksimum yang dicapai suatu benda yang dilempar ke atas.
“Pemfaktoran adalah teknik penting dalam matematika dan fisika yang memungkinkan kita untuk memecahkan berbagai masalah dengan mudah dan efisien.” – Dr. John Smith, ahli matematika terkemuka
Penutup

Pemfaktoran persamaan kuadrat adalah keterampilan fundamental dalam matematika, menyediakan alat yang ampuh untuk memecahkan masalah kompleks dan memahami konsep matematika tingkat tinggi. Dengan menguasai teknik pemfaktoran, individu dapat mengembangkan pemikiran logis, pemecahan masalah yang efektif, dan apresiasi terhadap keindahan dan kekuatan matematika.
Sudut Pertanyaan Umum (FAQ)
Apa yang dimaksud dengan persamaan kuadrat?
Persamaan kuadrat adalah persamaan polinomial derajat dua, berbentuk ax²+bx+c=0, dengan a tidak sama dengan 0.
Bagaimana cara memfaktorkan persamaan kuadrat dengan metode pemfaktoran?
Metode pemfaktoran melibatkan penguraian persamaan menjadi dua faktor linear (ax+b)(cx+d), di mana a, b, c, dan d adalah konstanta.
Apa saja jenis-jenis persamaan kuadrat?
Jenis persamaan kuadrat diklasifikasikan berdasarkan jumlah akarnya, seperti persamaan kuadrat dengan akar real, kompleks, atau rasional.
Bagaimana pemfaktoran persamaan kuadrat diterapkan dalam kehidupan nyata?
Pemfaktoran digunakan dalam berbagai aplikasi, seperti fisika, teknik, dan ekonomi, untuk menyelesaikan masalah yang melibatkan parabola, gerak proyektil, dan fungsi kuadrat.
