Dalam dunia matematika, sistem persamaan linear memainkan peran penting dalam menyelesaikan berbagai permasalahan. Sistem ini melibatkan sekumpulan persamaan yang mengandung variabel yang tidak diketahui, dan menemukan solusi mereka sangat penting untuk mengungkap hubungan antar variabel dan menarik kesimpulan yang bermakna.

Tulisan ini akan mengupas secara mendalam tentang sistem persamaan linear, metode penyelesaiannya, sifat solusi, dan aplikasi praktisnya. Selain itu, kami juga akan mengeksplorasi peran alat bantu komputer dalam memfasilitasi proses penyelesaian.

Definisi dan Konsep Sistem Persamaan Linear

Sistem persamaan linear adalah kumpulan dua atau lebih persamaan yang mengandung variabel yang sama dan disusun dalam bentuk persamaan linear. Persamaan linear adalah persamaan yang pangkat tertinggi variabelnya adalah satu.

Contoh sistem persamaan linear:

• 2x + 3y = 11
• x
  – y = 5

Sifat-sifat sistem persamaan linear:

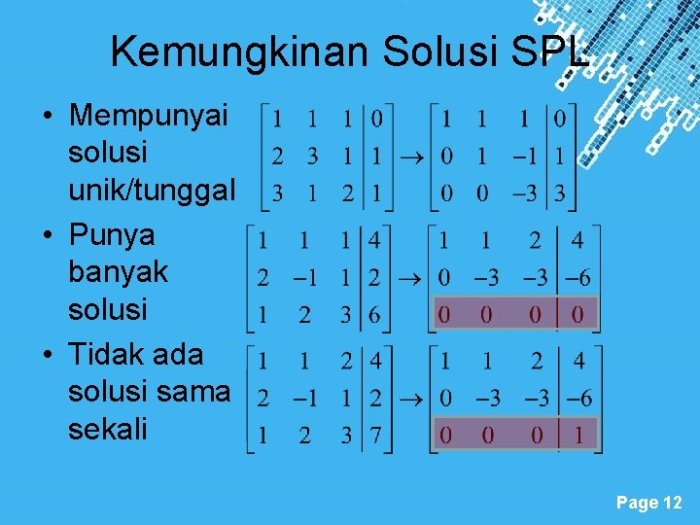
• Memiliki solusi tak hingga jika sistem konsisten (semua persamaan bergantung secara linier).
• Tidak memiliki solusi jika sistem inkonsisten (setidaknya satu persamaan tidak bergantung secara linier pada persamaan lainnya).
• Memiliki solusi tunggal jika sistem ekuivalen (semua persamaan mewakili persamaan yang sama).

Aplikasi Sistem Persamaan Linear

Sistem persamaan linear memiliki banyak aplikasi dalam kehidupan nyata. Sistem ini dapat digunakan untuk memecahkan berbagai masalah di bidang-bidang seperti ekonomi, fisika, teknik, dan ilmu komputer.

Contoh Aplikasi dalam Kehidupan Nyata

• Menentukan harga barang dan jasa dalam sistem ekonomi.
• Menghitung kecepatan dan percepatan benda dalam fisika.
• Mendesain struktur dan sistem teknik yang kompleks.
• Mengembangkan algoritma dan program komputer yang efisien.

Penggunaan Sistem Persamaan Linear untuk Memecahkan Masalah

Sistem persamaan linear dapat digunakan untuk memecahkan masalah dengan cara memodelkan situasi atau sistem yang sedang dipelajari sebagai sistem persamaan. Dengan memecahkan sistem tersebut, dapat diperoleh nilai variabel yang tidak diketahui, yang mewakili solusi dari masalah.

Ilustrasi Aplikasi

Misalnya, dalam ekonomi, sistem persamaan linear dapat digunakan untuk menentukan harga barang dan jasa dalam sistem ekonomi. Sistem ini dapat memodelkan hubungan antara penawaran dan permintaan, dan memecahkan sistem tersebut dapat menghasilkan harga yang menyeimbangkan pasar.

Dalam fisika, sistem persamaan linear dapat digunakan untuk menghitung kecepatan dan percepatan benda. Sistem ini dapat memodelkan hubungan antara kecepatan, percepatan, dan waktu, dan memecahkan sistem tersebut dapat menghasilkan nilai kecepatan dan percepatan benda.

Sifat dan Karakteristik Solusi Sistem Persamaan Linear

Sistem persamaan linear memiliki sifat-sifat solusi yang mempengaruhi jumlah dan jenis solusi yang dimilikinya.

Konsistensi

• Sistem persamaan linear konsisten jika memiliki setidaknya satu solusi.
• Sistem persamaan linear tidak konsisten jika tidak memiliki solusi.

Independensi dan Ketergantungan

• Sistem persamaan linear independen jika setiap persamaan memberikan informasi unik yang tidak dapat diperoleh dari persamaan lainnya.
• Sistem persamaan linear bergantung jika salah satu persamaan dapat diturunkan dari persamaan lainnya.

Sifat-sifat ini dapat mempengaruhi jumlah solusi sistem persamaan linear sebagai berikut:

• Sistem konsisten yang independen memiliki satu solusi unik.
• Sistem konsisten yang bergantung memiliki banyak solusi tak hingga.
• Sistem tidak konsisten tidak memiliki solusi.

Contoh

• Sistem persamaan linear konsisten dan independen:
  • x + y = 3
  • 2x
    – y = 1
• Sistem persamaan linear konsisten dan bergantung:
  • x + y = 3
  • 2x + 2y = 6
• Sistem persamaan linear tidak konsisten:
  • x + y = 3
  • x + y = 5

Alat Bantu Komputer untuk Menyelesaikan Sistem Persamaan Linear

Kemajuan teknologi telah mempermudah penyelesaian sistem persamaan linear yang kompleks. Alat bantu komputer, seperti perangkat lunak dan aplikasi, telah menjadi alat yang ampuh untuk memecahkan sistem ini dengan efisiensi dan akurasi yang tinggi.

Perangkat Lunak dan Aplikasi

• MATLAB: Platform komputasi numerik yang banyak digunakan untuk menyelesaikan sistem persamaan linear dan masalah aljabar lainnya.
• Python: Bahasa pemrograman serbaguna yang menawarkan pustaka seperti NumPy dan SciPy untuk operasi matriks dan penyelesaian sistem persamaan linear.
• Wolfram Mathematica: Sistem komputasi simbolik yang menyediakan fungsi bawaan untuk memecahkan sistem persamaan linear dan melakukan operasi matematika lainnya.
• Microsoft Excel: Program spreadsheet yang menyediakan fitur “Solver” untuk menyelesaikan sistem persamaan linear secara numerik.

Kelebihan dan Kekurangan

Meskipun alat bantu komputer menawarkan kemudahan dan efisiensi, ada juga beberapa kelebihan dan kekurangan yang perlu dipertimbangkan:

• Kelebihan
  • Otomatisasi proses penyelesaian
  • Kemampuan untuk menangani sistem persamaan yang kompleks
  • Penyediaan solusi yang akurat dan efisien
• Kekurangan
  • Ketergantungan pada perangkat lunak yang mungkin memerlukan lisensi atau pembelian
  • Potensi kesalahan jika perangkat lunak tidak digunakan dengan benar
  • Keterbatasan dalam menangani sistem persamaan yang sangat besar atau tidak linier

Ringkasan Terakhir

Memahami solusi sistem persamaan linear merupakan keterampilan penting dalam berbagai bidang, mulai dari ilmu pengetahuan hingga ekonomi. Dengan menguasai konsep dan metode yang diuraikan dalam tulisan ini, individu dapat memperoleh kemampuan untuk menganalisis dan menyelesaikan masalah kompleks, serta menarik kesimpulan yang tepat.

Sudut Pertanyaan Umum (FAQ)

Apa itu sistem persamaan linear?

Sistem persamaan linear adalah sekumpulan persamaan yang mengandung variabel tidak diketahui, di mana setiap persamaan dinyatakan dalam bentuk ax + by = c, dengan a, b, dan c sebagai konstanta.

Apa saja metode untuk menyelesaikan sistem persamaan linear?

Metode umum untuk menyelesaikan sistem persamaan linear meliputi eliminasi Gauss, substitusi, dan matriks.

Apa saja sifat solusi sistem persamaan linear?

Sifat solusi sistem persamaan linear meliputi konsistensi, independensi, dan ketergantungan, yang memengaruhi jumlah dan jenis solusi.

Apa saja aplikasi praktis sistem persamaan linear?

Sistem persamaan linear banyak digunakan dalam berbagai bidang, seperti fisika, teknik, ekonomi, dan ilmu komputer, untuk memecahkan masalah yang melibatkan hubungan antar variabel.

Apa saja kelebihan dan kekurangan menggunakan alat bantu komputer untuk menyelesaikan sistem persamaan linear?

Alat bantu komputer menawarkan kecepatan dan akurasi dalam menyelesaikan sistem persamaan linear, tetapi juga memiliki keterbatasan, seperti kebutuhan akan pemahaman dasar tentang perangkat lunak dan potensi kesalahan input.