Dalam matematika, barisan aritmatika merupakan urutan bilangan yang memiliki perbedaan yang sama antara suku-suku yang berdekatan. Pemahaman konsep ini sangat penting untuk menentukan suku ke-n dari barisan aritmatika, yang dapat diaplikasikan pada berbagai permasalahan.

Dalam artikel ini, kita akan mengulas konsep barisan aritmatika, merumuskan suku ke-n, dan mengaplikasikannya pada barisan tertentu, yaitu 5, 9, 13, 17. Selain itu, kita juga akan memberikan contoh tambahan dan membuat ilustrasi untuk memperjelas pemahaman.

Barisan Aritmatika

Barisan aritmatika adalah suatu barisan bilangan yang selisih antara dua suku yang berurutan selalu sama. Selisih ini disebut beda.

Rumus suku ke-n barisan aritmatika adalah:

Un = a + (n-1)b

di mana:

• Un adalah suku ke-n
• a adalah suku pertama
• b adalah beda
• n adalah nomor urut suku

Contoh Barisan Aritmatika

Selain barisan 5, 9, 13, 17 yang diberikan, berikut adalah contoh barisan aritmatika lainnya:

• 1, 3, 5, 7, 9, … (beda = 2)
• 10, 8, 6, 4, 2, … (beda =
  -2)
• 12, 15, 18, 21, 24, … (beda = 3)

Suku ke-n Barisan Aritmatika

Barisan aritmatika adalah barisan bilangan yang selisih antar sukunya sama. Rumus suku ke-n barisan aritmatika digunakan untuk menentukan suku ke-n dalam barisan aritmatika.

Rumus Suku ke-n Barisan Aritmatika

Rumus suku ke-n barisan aritmatika adalah sebagai berikut:

$$U_n = a + (n

1)b$$

di mana:* $$U_n$$ adalah suku ke-n

• $$a$$ adalah suku pertama
• $$b$$ adalah beda
• $$n$$ adalah nomor suku

Penggunaan Rumus

Rumus suku ke-n barisan aritmatika dapat digunakan untuk mencari suku ke-n dalam barisan aritmatika. Langkah-langkahnya adalah sebagai berikut:

1. Tentukan suku pertama ($$a$$) dan beda ($$b$$) barisan aritmatika.
2. Substitusikan nilai $$a$$, $$b$$, dan $$n$$ ke dalam rumus suku ke-n.
3. Hitung nilai $$U_n$$.

Penerapan pada Barisan Tertentu

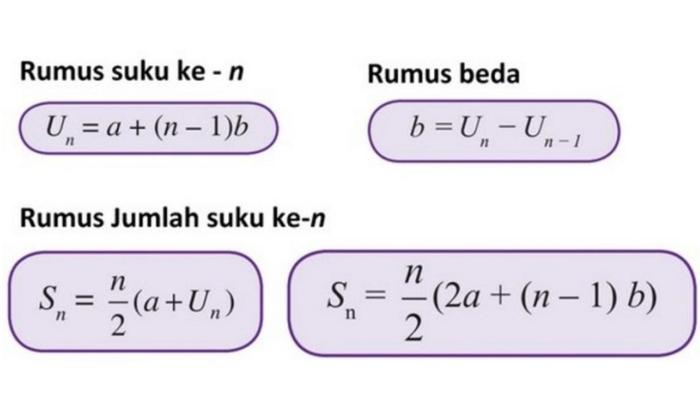
Barisan aritmatika adalah barisan bilangan yang selisih antara dua suku berurutannya selalu sama. Untuk menentukan suku ke-n dari barisan aritmatika, kita perlu mengidentifikasi beda barisan dan suku pertama.

Dalam kasus barisan (5, 9, 13, 17), beda barisan adalah 4 karena setiap suku berurutan berselisih 4. Suku pertama barisan adalah 5.

Menghitung Suku ke-n

Rumus untuk menghitung suku ke-n (Un) dari barisan aritmatika adalah:

Un = a + (n

• 1)
• b

di mana:

• a adalah suku pertama
• b adalah beda barisan
• n adalah nomor suku

Untuk menghitung suku ke-n dari barisan (5, 9, 13, 17), kita substitusikan a = 5, b = 4, dan n ke dalam rumus:

Un = 5 + (n

• 1)
• 4

Contoh Tambahan

Berikut adalah contoh lain dari barisan aritmatika dan cara menghitung suku ke-n-nya:

Barisan Aritmatika Alternatif

• Barisan: 3, 7, 11, 15, …
• Suku pertama (a): 3
• Beda (b): 4
• Suku ke-n (Un): Un = a + (n
  – 1)b
• Suku ke-5 (U5): U5 = 3 + (5
  – 1)4 = 3 + 16 = 19

Ilustrasi

Diagram Barisan Aritmatika

Barisan aritmatika dapat digambarkan sebagai serangkaian titik yang berjarak sama pada garis bilangan. Suku pertama (a) mewakili titik awal barisan, sedangkan beda (b) mewakili jarak antara suku-suku yang berurutan.

Misalnya, barisan aritmatika 5, 9, 13, 17 dapat digambarkan sebagai berikut:

Rumus Suku ke-n

Suku ke-n (Un) dalam barisan aritmatika dapat dicari menggunakan rumus berikut:

Un = a + (n

1)b

Dimana:

• Un adalah suku ke-n
• a adalah suku pertama
• n adalah nomor urut suku
• b adalah beda barisan

Ringkasan Penutup

Dengan memahami konsep suku ke-n dari barisan aritmatika, kita dapat menyelesaikan berbagai permasalahan yang melibatkan barisan bilangan. Rumus yang telah dibahas dapat diaplikasikan pada barisan aritmatika apa pun, sehingga sangat berguna dalam bidang matematika dan sains.

Pertanyaan Umum yang Sering Muncul

Apa itu barisan aritmatika?

Barisan aritmatika adalah urutan bilangan yang memiliki perbedaan yang sama antara suku-suku yang berdekatan.

Bagaimana cara menentukan suku ke-n dari barisan aritmatika?

Suku ke-n dari barisan aritmatika dapat ditentukan menggunakan rumus Un = a + (n-1)b, di mana a adalah suku pertama, b adalah beda, dan n adalah nomor suku.

Apa beda dari barisan aritmatika 5, 9, 13, 17?

Beda dari barisan aritmatika 5, 9, 13, 17 adalah 4.