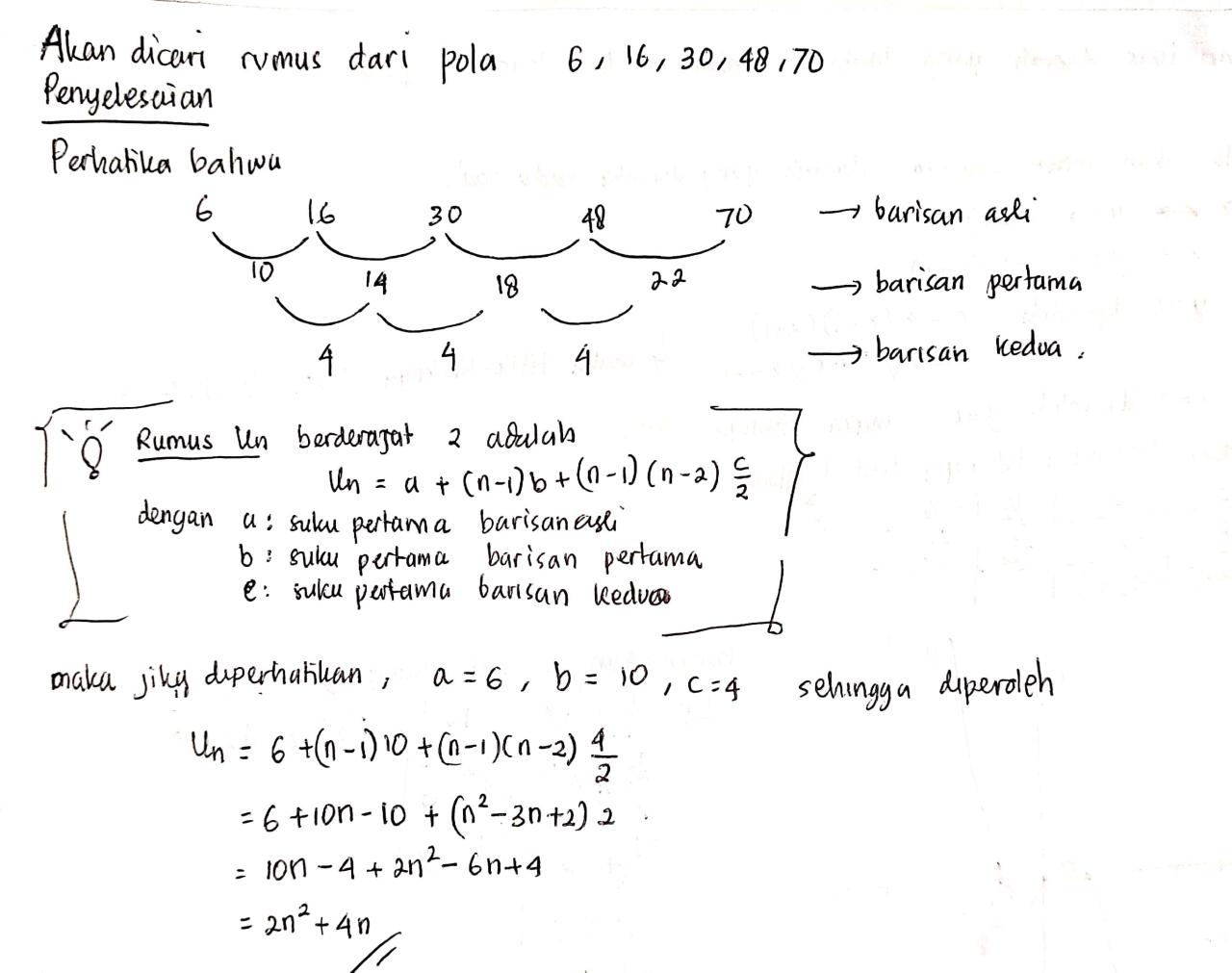
Suku tengah dari barisan 3 8 13 103 adalah – Dalam matematika, konsep suku tengah barisan aritmatika memainkan peran penting dalam memahami pola bilangan dan melakukan berbagai perhitungan. Suku tengah suatu barisan aritmatika memberikan wawasan tentang nilai rata-rata dan sifat keseluruhan barisan.
Barisan aritmatika adalah barisan bilangan yang selisih antar suku-sukunya konstan. Dalam barisan 3, 8, 13, …, 103, selisih antar suku adalah 5. Suku tengah barisan ini akan memberikan informasi penting tentang barisan secara keseluruhan.
Konsep Suku Tengah Barisan Aritmatika
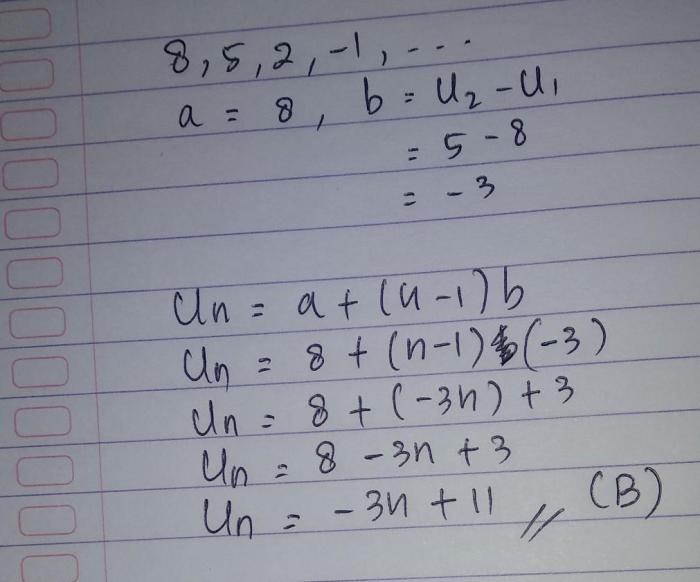
Suku tengah suatu barisan aritmatika adalah suku yang terletak di tengah-tengah barisan, membagi barisan menjadi dua bagian yang sama.
Untuk mencari suku tengah barisan aritmatika, dapat digunakan rumus berikut:
Suku tengah = (Jumlah suku pertama dan terakhir) / 2
Contohnya, untuk barisan aritmatika 3, 8, 13, 18, 23, jumlah suku pertama dan terakhir adalah 3 + 23 = 26. Oleh karena itu, suku tengahnya adalah (26) / 2 = 13.
Rumus Mencari Suku Tengah, Suku tengah dari barisan 3 8 13 103 adalah
- Suku tengah = (Jumlah suku pertama dan terakhir) / 2
- Jumlah suku pertama dan terakhir = Suku pertama + Suku terakhir
Contoh Aplikasi
Misalkan suatu barisan aritmatika memiliki suku pertama 5 dan suku terakhir 25. Berapakah suku tengahnya?
Jumlah suku pertama dan terakhir: 5 + 25 = 30
Suku tengah dari barisan 3, 8, 13, 103 adalah 8. Perkembangan teknologi transportasi yang pesat, seperti contoh perkembangan teknologi transportasi mobil listrik dan kereta cepat, telah memudahkan mobilitas manusia. Kemajuan ini turut mempengaruhi cara pandang kita terhadap suku tengah barisan, yang kini tidak lagi hanya terbatas pada konteks matematika tetapi juga mencakup konteks kehidupan nyata.
Suku tengah: 30 / 2 = 15
Jadi, suku tengah barisan aritmatika tersebut adalah 15.
Rumus Suku Tengah Barisan Aritmatika
Dalam barisan aritmatika, suku tengah adalah suku yang terletak di tengah barisan. Rumus untuk menghitung suku tengah barisan aritmatika adalah sebagai berikut:
Cara Menghitung Suku Tengah
Untuk menghitung suku tengah barisan aritmatika, gunakan rumus berikut:
Sn = (n+1)/2 x (a + an)
- Sn adalah suku tengah barisan aritmatika
- n adalah jumlah suku dalam barisan
- a adalah suku pertama barisan
- an adalah suku terakhir barisan
Identifikasi Suku Tengah dari Barisan Tertentu
Untuk mengidentifikasi suku tengah dari suatu barisan, kita perlu memahami konsep suku tengah dan rumus yang digunakan untuk menghitungnya.
Menentukan Suku Tengah
Suku tengah adalah suku yang terletak di tengah-tengah suatu barisan. Untuk menentukan suku tengah, kita perlu mengetahui jumlah suku dalam barisan tersebut.
Rumus untuk menghitung jumlah suku dalam barisan adalah:
Jumlah suku = (Suku terakhir
Suku pertama) / Selisih + 1
Setelah mengetahui jumlah suku, kita dapat menentukan suku tengah menggunakan rumus berikut:
Suku tengah = (Jumlah suku + 1) / 2
Contoh: Barisan 3, 8, 13, …, 103
Untuk barisan 3, 8, 13, …, 103, kita dapat menghitung jumlah suku terlebih dahulu:
Jumlah suku = (103 – 3) / 5 + 1 = 21
Selanjutnya, kita dapat menghitung suku tengah:
Suku tengah = (21 + 1) / 2 = 11
Jadi, suku tengah dari barisan 3, 8, 13, …, 103 adalah suku ke-11.
Sifat-Sifat Suku Tengah

Suku tengah pada barisan aritmatika memiliki sifat-sifat tertentu yang dapat membantu kita memahaminya dengan lebih baik.
Ganjil/Genap
Suku tengah barisan aritmatika selalu ganjil jika jumlah suku ganjil dan genap jika jumlah suku genap. Hal ini karena suku tengah merupakan nilai tengah dari semua suku, dan nilai tengah selalu ganjil untuk jumlah suku ganjil dan genap untuk jumlah suku genap.
Hubungan dengan Jumlah Suku
Suku tengah barisan aritmatika juga memiliki hubungan dengan jumlah suku. Untuk jumlah suku ganjil (n = 2m + 1), suku tengah adalah suku ke-m + 1. Sedangkan untuk jumlah suku genap (n = 2m), suku tengah adalah rata-rata dari suku ke-m dan suku ke-m + 1.
Suku tengah dari barisan 3 8 13 103 adalah 8. Jika kita kaitkan dengan peta penyebaran manusia purba di indonesia , suku tengah ini dapat mengindikasikan lokasi temuan fosil manusia purba tertentu. Misalnya, temuan fosil Homo floresiensis di Liang Bua, Flores, berada di sekitar suku tengah barisan 3 8 13 103. Hal ini menunjukkan adanya hubungan antara penyebaran manusia purba dengan suku tengah barisan tersebut.
Contoh
Pada barisan aritmatika 3, 8, 13, …, suku tengahnya adalah 13 karena jumlah suku ganjil (n = 3). Sedangkan pada barisan aritmatika 1, 3, 5, …, suku tengahnya adalah 4 karena jumlah suku genap (n = 4) dan merupakan rata-rata dari suku ke-2 dan suku ke-3.
Aplikasi Suku Tengah dalam Matematika
Suku tengah memiliki berbagai aplikasi dalam matematika, terutama dalam menghitung rata-rata dan menjumlahkan deret aritmatika.
Menghitung Rata-rata
Rata-rata suatu himpunan data dapat dihitung dengan menjumlahkan semua nilai data dan membagi hasilnya dengan jumlah data. Suku tengah dapat digunakan untuk menghitung rata-rata suatu deret aritmatika dengan cepat dan efisien.
Menjumlahkan Deret Aritmatika
Deret aritmatika adalah suatu barisan bilangan di mana beda antara dua suku yang berurutan adalah sama. Jumlah suku suatu deret aritmatika dapat dihitung menggunakan suku tengah. Rumus untuk menjumlahkan deret aritmatika adalah:
Sn = n/2- (a1 + an)
di mana Sn adalah jumlah suku, n adalah jumlah suku, a1 adalah suku pertama, dan an adalah suku terakhir.
Kesimpulan: Suku Tengah Dari Barisan 3 8 13 103 Adalah

Suku tengah barisan aritmatika memberikan informasi penting tentang nilai rata-rata dan sifat barisan.
Rumus suku tengah memungkinkan kita menentukan suku tengah tanpa menghitung semua suku sebelumnya, menjadikannya alat yang berguna dalam analisis barisan aritmatika.
Suku tengah dari barisan 3, 8, 13, 103 adalah 8. Menariknya, dalam dunia elektromagnetisme, penentuan kutub magnet elektromagnet juga memiliki teknik tersendiri. Dengan memahami cara menentukan kutub magnet elektromagnet , kita dapat mengidentifikasi polaritas magnet yang dihasilkan oleh aliran listrik.
Kembali ke barisan awal, suku tengah 8 merupakan nilai yang memisahkan deret bilangan menjadi dua bagian yang simetris, sehingga memberikan gambaran keseimbangan dan simetri dalam suatu barisan bilangan.
Sifat Suku Tengah
Suku tengah barisan aritmatika memiliki sifat sebagai berikut:
- Untuk barisan genap, suku tengah adalah rata-rata dari dua suku tengah.
- Untuk barisan ganjil, suku tengah adalah suku yang berada di tengah barisan.
Rumus Suku Tengah
Rumus suku tengah barisan aritmatika adalah:
Sn= a + (n
1)d
di mana:
- S nadalah suku tengah
- a adalah suku pertama
- n adalah jumlah suku
- d adalah beda
Kegunaan Rumus Suku Tengah
Rumus suku tengah memiliki beberapa kegunaan praktis, antara lain:
- Menentukan nilai rata-rata barisan aritmatika
- Memprediksi nilai suku yang hilang dalam barisan aritmatika
- Menentukan jumlah suku tertentu dalam barisan aritmatika
Pemungkas

Dengan menggunakan rumus suku tengah, kita dapat menentukan bahwa suku tengah barisan 3, 8, 13, …, 103 adalah 53. Pemahaman tentang suku tengah barisan aritmatika sangat penting dalam berbagai aplikasi matematika, seperti menghitung rata-rata dan menjumlahkan deret aritmatika.
Pertanyaan Umum (FAQ)
Apa itu suku tengah barisan aritmatika?
Suku tengah barisan aritmatika adalah suku yang terletak di tengah barisan ketika jumlah suku ganjil. Jika jumlah suku genap, maka tidak ada suku tengah.
Bagaimana cara menghitung suku tengah barisan aritmatika?
Suku tengah barisan aritmatika dapat dihitung menggunakan rumus Sn = a + (n-1)b, di mana Sn adalah suku tengah, a adalah suku pertama, n adalah jumlah suku, dan b adalah beda.
Apa saja sifat-sifat suku tengah barisan aritmatika?
Suku tengah barisan aritmatika selalu ganjil jika jumlah suku ganjil. Jika jumlah suku genap, maka tidak ada suku tengah. Selain itu, suku tengah merupakan rata-rata dari dua suku yang berdekatan dengannya.