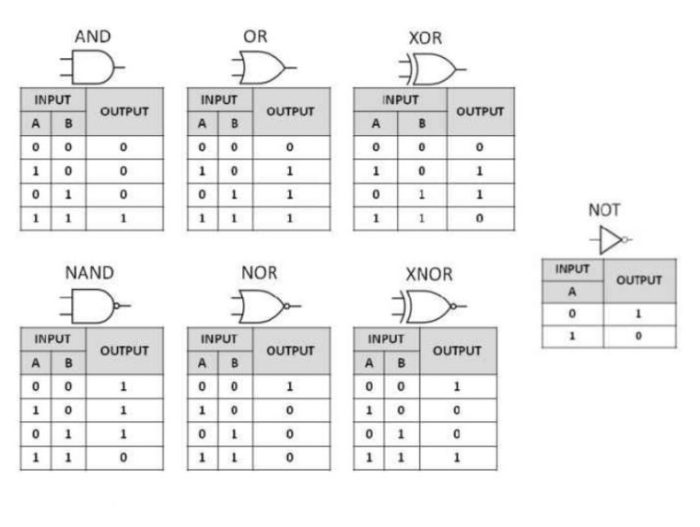
Dalam ranah logika, tabel kebenaran memainkan peran penting sebagai alat yang ampuh untuk mengevaluasi ekspresi logika. Tabel kebenaran untuk 4 variabel, khususnya, memberikan wawasan yang mendalam tentang interaksi variabel-variabel tersebut, mengungkap hubungan kompleks yang mendasari operasi logika.

Konsep tabel kebenaran berakar pada gagasan nilai kebenaran, di mana setiap variabel dapat mengambil nilai benar atau salah. Dengan menggabungkan nilai-nilai kebenaran ini secara sistematis, tabel kebenaran memberikan representasi lengkap dari semua kemungkinan kombinasi nilai kebenaran untuk variabel yang diberikan.

Tabel Kebenaran 4 Variabel

Dalam logika, tabel kebenaran digunakan untuk mengevaluasi nilai kebenaran ekspresi logika untuk semua kombinasi nilai input yang mungkin. Tabel kebenaran untuk 4 variabel terdiri dari 16 baris, mewakili semua kombinasi yang mungkin dari nilai benar (1) dan salah (0) untuk 4 variabel.

Tabel kebenaran 4 variabel dapat digunakan untuk mengevaluasi ekspresi logika yang melibatkan 4 variabel. Setiap baris dalam tabel mewakili satu kombinasi nilai input, dan kolom untuk setiap variabel menunjukkan nilai kebenaran variabel tersebut untuk kombinasi itu.

Membuat Tabel Kebenaran 4 Variabel

Untuk membuat tabel kebenaran 4 variabel, ikuti langkah-langkah berikut:

1. Daftar semua kemungkinan kombinasi nilai input untuk 4 variabel.
2. Buat kolom untuk setiap variabel dan kolom untuk nilai kebenaran ekspresi.
3. Isi kolom variabel dengan semua kombinasi nilai input yang mungkin.
4. Evaluasi ekspresi untuk setiap kombinasi nilai input dan isi kolom nilai kebenaran dengan hasilnya.

Menggunakan Tabel Kebenaran untuk Mengevaluasi Ekspresi Logika

Tabel kebenaran dapat digunakan untuk mengevaluasi nilai kebenaran ekspresi logika dengan memeriksa baris yang sesuai dengan kombinasi nilai input yang diberikan. Misalnya, untuk mengevaluasi ekspresi (A ∨ B) ∧ C, cari baris dalam tabel kebenaran di mana A dan B bernilai benar (1) dan C bernilai salah (0). Nilai kebenaran ekspresi untuk kombinasi nilai input ini adalah salah (0), karena ekspresi hanya bernilai benar jika A atau B dan C bernilai benar.

Contoh Tabel Kebenaran 4 Variabel

Tabel kebenaran merupakan alat yang digunakan dalam logika matematika untuk menentukan nilai kebenaran dari suatu pernyataan majemuk yang mengandung beberapa variabel proposisi. Tabel kebenaran menunjukkan semua kemungkinan kombinasi nilai kebenaran dari variabel-variabel tersebut dan nilai kebenaran pernyataan majemuk yang dihasilkan.

Tabel Kebenaran untuk 4 Variabel

Sebagai contoh, berikut adalah tabel kebenaran untuk 4 variabel proposisi P, Q, R, dan S:| P | Q | R | S | P ∧ Q ∧ R ∧ S ||—|—|—|—|—|| T | T | T | T | T || T | T | T | F | F || T | T | F | T | F || T | T | F | F | F || T | F | T | T | F || T | F | T | F | F || T | F | F | T | F || T | F | F | F | F || F | T | T | T | F || F | T | T | F | F || F | T | F | T | F || F | T | F | F | F || F | F | T | T | F || F | F | T | F | F || F | F | F | T | F || F | F | F | F | F |

Cara Membuat Tabel Kebenaran 4 Variabel

Tabel kebenaran adalah tabel yang menampilkan semua kemungkinan kombinasi nilai kebenaran dari variabel-variabel yang diberikan. Tabel kebenaran untuk 4 variabel memiliki 16 baris, karena setiap variabel dapat bernilai benar atau salah.

Langkah-langkah Membuat Tabel Kebenaran 4 Variabel

1. Tentukan variabel-variabel yang terlibat.
2. Buat kolom untuk setiap variabel, dengan label “Benar” dan “Salah”.
3. Tuliskan semua kemungkinan kombinasi nilai kebenaran variabel-variabel tersebut di kolom.
4. Untuk setiap baris, tentukan nilai kebenaran untuk ekspresi yang diberikan.
5. Tuliskan nilai kebenaran yang ditentukan di kolom yang sesuai.

Contoh

Misalkan kita ingin membuat tabel kebenaran untuk ekspresi berikut:

“`(A ∨ B) ∧ (C ∨ D)“`

Langkah-langkah pembuatan tabel kebenaran:

1. Variabel-variabel yang terlibat: A, B, C, D.
2. Kolom: A (Benar/Salah), B (Benar/Salah), C (Benar/Salah), D (Benar/Salah), (A ∨ B) (Benar/Salah), (C ∨ D) (Benar/Salah), (A ∨ B) ∧ (C ∨ D) (Benar/Salah).
3. Kombinasi nilai kebenaran: 16 baris (2^4).
4. Nilai kebenaran untuk setiap baris:
• Baris 1: (A = Benar, B = Benar, C = Benar, D = Benar)
  -> (A ∨ B) = Benar, (C ∨ D) = Benar, (A ∨ B) ∧ (C ∨ D) = Benar
• Baris 2: (A = Benar, B = Benar, C = Benar, D = Salah)
  -> (A ∨ B) = Benar, (C ∨ D) = Benar, (A ∨ B) ∧ (C ∨ D) = Benar
• …
5. Tabel kebenaran yang lengkap:

A	B	C	D	(A ∨ B)	(C ∨ D)	(A ∨ B) ∧ (C ∨ D)
Benar	Benar	Benar	Benar	Benar	Benar	Benar
Benar	Benar	Benar	Salah	Benar	Benar	Benar
…	…	…	…	…	…	…

Prosedur Menggunakan Tabel Kebenaran 4 Variabel

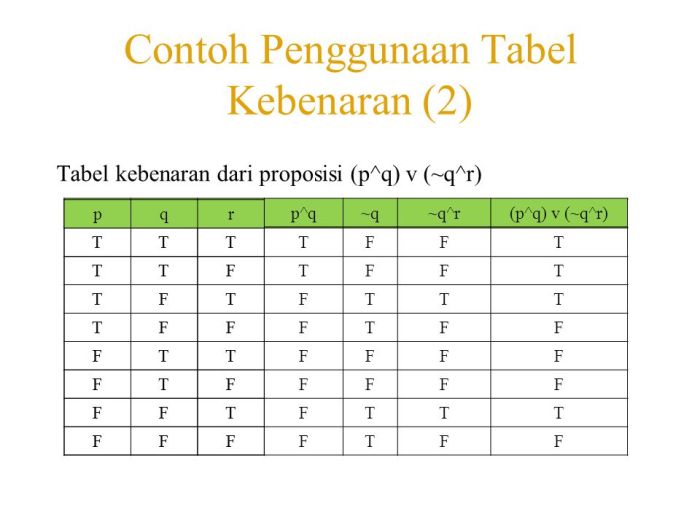
Untuk mengevaluasi ekspresi logika dengan 4 variabel menggunakan tabel kebenaran, ikuti prosedur berikut:

Susun Kolom Variabel

• Buat kolom untuk setiap variabel (misalnya, P, Q, R, S).
• Isi setiap kolom dengan nilai kebenaran “benar” (T) dan “salah” (F).

Tentukan Semua Kemungkinan Kombinasi

• Untuk 4 variabel, ada 2⁴ = 16 kemungkinan kombinasi nilai kebenaran.
• Buat baris untuk setiap kombinasi, mengisi kolom variabel dengan nilai kebenaran yang sesuai.

Evaluasi Ekspresi Logika

• Gunakan operasi logika (AND, OR, NOT) untuk mengevaluasi ekspresi untuk setiap baris.
• Isi kolom tambahan dengan nilai kebenaran hasil dari ekspresi logika.

Kasus Khusus

Dalam beberapa kasus, tabel kebenaran mungkin memiliki kasus khusus:

• Kontradiksi: Ekspresi yang selalu bernilai salah, terlepas dari nilai variabelnya.
• Tautologi: Ekspresi yang selalu bernilai benar, terlepas dari nilai variabelnya.

Penerapan Tabel Kebenaran 4 Variabel

Tabel kebenaran 4 variabel memiliki aplikasi yang luas dalam logika dan matematika, menyediakan cara sistematis untuk mengevaluasi proposisi kompleks dengan banyak variabel.

Aplikasi dalam Logika

• Memeriksa validitas argumen: Tabel kebenaran dapat digunakan untuk menentukan apakah suatu argumen valid, yaitu apakah kesimpulan mengikuti secara logis dari premisnya.
• Menyederhanakan ekspresi logika: Dengan menggunakan sifat-sifat distributif dan asosiatif, tabel kebenaran dapat digunakan untuk menyederhanakan ekspresi logika menjadi bentuk yang lebih sederhana.
• Membangun sirkuit logika: Tabel kebenaran dapat digunakan untuk merancang sirkuit logika yang mengimplementasikan fungsi logika tertentu.

Aplikasi dalam Matematika

• Menyelesaikan persamaan boolean: Tabel kebenaran dapat digunakan untuk menyelesaikan persamaan boolean dengan beberapa variabel, yang dapat berguna dalam aljabar dan ilmu komputer.
• Membuat fungsi logika: Tabel kebenaran dapat digunakan untuk menentukan nilai suatu fungsi logika untuk semua kombinasi input yang mungkin.
• Menganalisis fungsi kombinasional: Dalam desain digital, tabel kebenaran digunakan untuk menganalisis dan mendiagnosis fungsi kombinasional dalam rangkaian logika.

Variasi dan Ekstensi Tabel Kebenaran

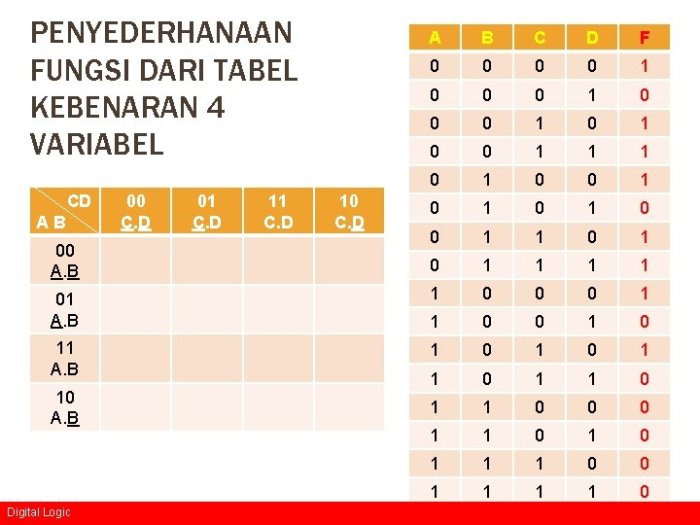
Tabel kebenaran merupakan alat penting dalam logika matematika yang menunjukkan nilai kebenaran suatu pernyataan majemuk untuk semua kemungkinan nilai kebenaran variabel penyusunnya. Namun, tabel kebenaran dapat divariasikan dan diperluas untuk menangani jumlah variabel yang berbeda dan tujuan yang lebih kompleks.

Ekstensi untuk Variabel Tambahan

Tabel kebenaran dapat diperluas untuk menampung jumlah variabel yang lebih banyak. Misalnya, tabel kebenaran untuk 5 variabel akan memiliki 32 baris, sementara tabel kebenaran untuk 10 variabel akan memiliki 1024 baris. Ekstensi ini memungkinkan kita untuk menganalisis pernyataan majemuk yang lebih kompleks dengan jumlah variabel yang lebih banyak.

Variasi untuk Proposisi dan Predikat

Selain menangani variabel proposisi (benar atau salah), tabel kebenaran juga dapat diperluas untuk menangani proposisi dan predikat. Proposisi adalah pernyataan yang dapat bernilai benar atau salah, sedangkan predikat adalah pernyataan yang bernilai benar atau salah tergantung pada argumennya. Tabel kebenaran untuk proposisi dan predikat dapat membantu kita menganalisis hubungan antara pernyataan dan argumennya.

Kelebihan dan Kekurangan Berbagai Pendekatan

Berbagai pendekatan untuk variasi dan ekstensi tabel kebenaran memiliki kelebihan dan kekurangannya masing-masing. Tabel kebenaran untuk jumlah variabel yang lebih banyak dapat menjadi sangat besar dan sulit untuk ditafsirkan, tetapi menyediakan analisis yang komprehensif. Tabel kebenaran untuk proposisi dan predikat lebih fleksibel, tetapi dapat menjadi lebih kompleks tergantung pada jumlah argumen yang terlibat.

Kesimpulan Akhir

Tabel kebenaran 4 variabel tidak hanya merupakan alat yang ampuh untuk evaluasi logika, tetapi juga dasar untuk memahami struktur operasi logika yang lebih kompleks. Dengan menyajikan semua kemungkinan kombinasi nilai kebenaran, tabel ini memfasilitasi analisis hubungan antara variabel, memungkinkan logika untuk diterapkan pada berbagai masalah dunia nyata.

Pertanyaan Umum (FAQ)

Apa saja langkah-langkah membuat tabel kebenaran 4 variabel?

Langkah-langkahnya meliputi: menentukan jumlah baris, menetapkan nilai kebenaran untuk setiap variabel, dan menghitung nilai kebenaran untuk setiap ekspresi logika.

Bagaimana cara menggunakan tabel kebenaran untuk mengevaluasi ekspresi logika?

Dengan mencari baris yang sesuai dengan kombinasi nilai kebenaran untuk variabel, kita dapat menentukan nilai kebenaran untuk ekspresi logika yang diberikan.

Apa kelebihan menggunakan tabel kebenaran?

Tabel kebenaran memberikan representasi lengkap dari semua kemungkinan kombinasi nilai kebenaran, membuatnya mudah untuk mengevaluasi ekspresi logika dan mengidentifikasi pola.