Tentukan hasil bagi bentuk aljabar berikut – Menentukan hasil bagi bentuk aljabar merupakan keterampilan penting dalam aljabar yang memungkinkan kita menyederhanakan ekspresi kompleks dan menyelesaikan berbagai masalah matematika. Artikel ini akan memberikan panduan komprehensif tentang cara menentukan hasil bagi bentuk aljabar, membahas konsep dasarnya, metode yang berbeda, dan kasus-kasus khusus.

Dalam aljabar, bentuk aljabar adalah ekspresi yang terdiri dari konstanta, variabel, dan operator. Hasil bagi bentuk aljabar mengacu pada hasil pembagian satu bentuk aljabar dengan bentuk aljabar lainnya, yang dapat memberikan wawasan berharga tentang struktur dan sifat bentuk aljabar.

Pemahaman Bentuk Aljabar

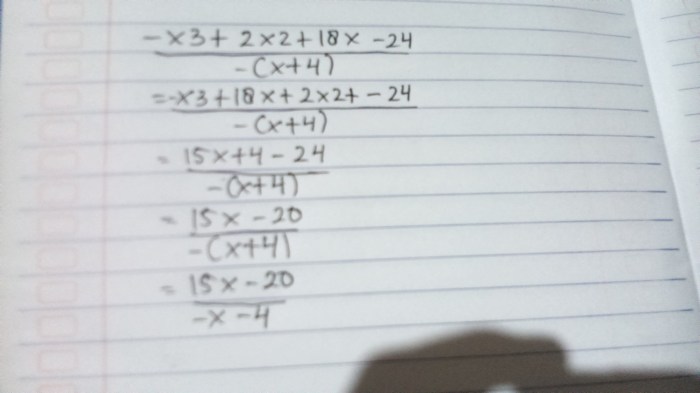
Bentuk aljabar adalah ekspresi matematika yang terdiri dari konstanta, variabel, dan operasi matematika. Konstanta adalah bilangan tetap, sedangkan variabel adalah simbol yang mewakili bilangan yang tidak diketahui.

Bentuk aljabar dapat sederhana, seperti x + 2, atau kompleks, seperti (x²– 4) / (x + 1) . Sifat-sifat operasi aljabar, seperti penjumlahan, pengurangan, perkalian, dan pembagian, memungkinkan kita memanipulasi bentuk aljabar untuk menyelesaikan persamaan dan pertidaksamaan.

Bagian-bagian Bentuk Aljabar

Bentuk aljabar memiliki beberapa bagian:

• Suku:Bagian terpisah dari bentuk aljabar yang dihubungkan oleh tanda tambah atau minus.
• Koefisien:Bilangan yang mengalikan variabel dalam suatu suku.
• Variabel:Simbol yang mewakili bilangan yang tidak diketahui.
• Konstanta:Bilangan yang tidak mengandung variabel.
• Eksponen:Bilangan kecil yang ditulis di atas variabel untuk menunjukkan pangkatnya.

Konsep Hasil Bagi Bentuk Aljabar

Hasil bagi bentuk aljabar adalah ekspresi aljabar yang dihasilkan ketika satu bentuk aljabar dibagi dengan bentuk aljabar lainnya. Hasil bagi ini menunjukkan berapa kali pembagi (bentuk aljabar yang membagi) terkandung dalam dividen (bentuk aljabar yang dibagi).

Langkah-langkah Menentukan Hasil Bagi Bentuk Aljabar

• Susun dividen dan pembagi dalam bentuk pembagian bersusun.
• Bagilah suku pertama dividen dengan suku pertama pembagi.
• Kalikan hasil bagi dengan pembagi dan kurangkan hasilnya dari dividen.
• Turunkan suku berikutnya dari dividen dan ulangi langkah 2-3.
• Lanjutkan proses ini sampai tidak ada lagi suku yang tersisa pada dividen.

Metode Menentukan Hasil Bagi Bentuk Aljabar

Ada beberapa metode untuk menentukan hasil bagi bentuk aljabar, antara lain:

• Pembagian Bersusun
• Pemfaktoran
• Teorema Sisa
• Teorema Faktor

Contoh

Tentukan hasil bagi dari bentuk aljabar berikut:

x³

• 2x ²+ x
• 2 dibagi (x
• 1)

Pembagian Bersusun:

“` x ²

x + 1

x

• 1 ) x ³
• 2x ²+ x
• 2

• (x ³
• x ²)

——–

x²+ x

(-x²+ x)

——–

0“`

Hasil bagi: x ²– x + 1

Aplikasi

Hasil bagi bentuk aljabar memiliki berbagai aplikasi dalam matematika, seperti:

• Menyederhanakan ekspresi aljabar
• Memecahkan persamaan
• Menentukan nol dari suatu polinomial

Cara Menentukan Hasil Bagi Bentuk Aljabar

Menentukan hasil bagi bentuk aljabar adalah proses menemukan ekspresi aljabar yang mewakili pembagian satu bentuk aljabar dengan bentuk aljabar lainnya.

Langkah-langkah Menentukan Hasil Bagi Bentuk Aljabar

Berikut adalah langkah-langkah umum untuk menentukan hasil bagi bentuk aljabar:

1. Susun bentuk aljabar sebagai dividen dan pembagi dalam bentuk pecahan.
2. Lakukan pembagian panjang seperti pada pembagian bilangan biasa, tetapi dengan menggunakan variabel sebagai pengganti angka.
3. Turunkan setiap suku dividen ke pembagi dan kalikan dengan suku pertama pembagi.
4. Kurangkan hasil perkalian dari dividen.
5. Tambahkan suku berikutnya dari dividen ke hasil pengurangan dan ulangi langkah 3 dan 4 hingga tidak ada suku lagi yang tersisa di dividen.
6. Hasil akhir dari pembagian panjang adalah hasil bagi bentuk aljabar.

Contoh

Misalkan kita ingin menentukan hasil bagi dari bentuk aljabar:

(x³

• 2x ²+ 3x
• 4) ÷ (x
• 2)

Dengan mengikuti langkah-langkah di atas, kita akan mendapatkan hasil bagi:

x²

x + 2

Prosedur Pembagian Bersusun: Tentukan Hasil Bagi Bentuk Aljabar Berikut

Pembagian bersusun adalah metode untuk membagi bentuk aljabar yang panjang. Ini adalah prosedur sistematis yang memecah proses menjadi langkah-langkah yang lebih kecil dan lebih mudah dikelola.

Dalam menentukan hasil bagi bentuk aljabar, pemahaman mengenai sifat-sifat operasi aljabar sangat penting. Barisan aritmatika, seperti suku tengah dari barisan 3 8 13 103 adalah , memiliki pola yang dapat membantu dalam menyelesaikan masalah aljabar. Dengan memahami konsep ini, individu dapat menguasai teknik menentukan hasil bagi bentuk aljabar secara efektif.

Ilustrasi Pembagian Bersusun

Pembagian bersusun dapat diilustrasikan sebagai berikut:

Dividend (Pembagi)   |   Divisor (Pembagi)

---

Kuosien

---

Sisa

Langkah-langkah Pembagian Bersusun

1. Bagi suku pertama dividen dengan suku pertama divisor.
2. Kalikan hasil bagi dengan seluruh divisor dan kurangi hasilnya dari dividen.
3. Turunkan suku berikutnya dari dividen.
4. Ulangi langkah 1-3 sampai tidak ada lagi suku yang tersisa di dividen.

Contoh Pembagian Bersusun

Bagilah bentuk aljabar x ³+ 2x ²– 5x + 6 dengan x + 1:

Hasil bagi adalah x ²+ x – 6.

Prosedur Pemfaktoran

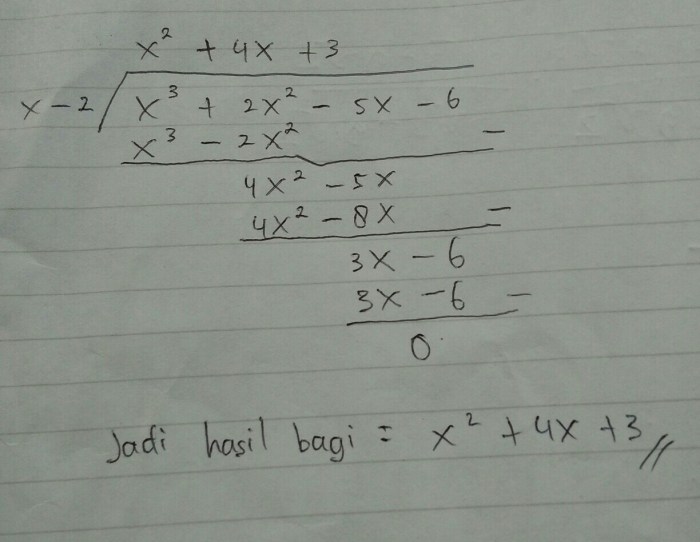
Pemfaktoran adalah proses menguraikan suatu bentuk aljabar menjadi faktor-faktor yang lebih sederhana. Hal ini berguna untuk menyelesaikan persamaan, menyederhanakan ekspresi, dan menyelesaikan masalah matematika lainnya.

Ada beberapa metode pemfaktoran yang umum digunakan, antara lain:

Pemfaktoran Persekutuan Terbesar (FPB)

FPB adalah faktor terbesar yang membagi dua atau lebih bilangan. Untuk memfaktorkan suatu bentuk aljabar menggunakan FPB, carilah faktor-faktor yang sama dari semua suku. Misalnya, untuk memfaktorkan 12x ²+ 6xy, FPB adalah 6x. Oleh karena itu, bentuk aljabar tersebut dapat difaktorkan menjadi 6x(2x + y).

Dalam menentukan hasil bagi bentuk aljabar, kita perlu memahami konsep dasar aljabar. Sama halnya dengan perbedaan musaqah muzara ah dan mukhabarah, yang merupakan bentuk kerja sama dalam pertanian perbedaan musaqah muzara ah dan mukhabarah . Kedua jenis kerja sama ini memiliki karakteristik yang berbeda, sama seperti proses menentukan hasil bagi bentuk aljabar yang melibatkan operasi matematika.

Pemfaktoran Selisih Kuadrat

Pemfaktoran selisih kuadrat digunakan untuk memfaktorkan bentuk aljabar yang memiliki bentuk a ²– b ². Bentuk ini dapat difaktorkan menjadi (a + b)(a – b). Misalnya, untuk memfaktorkan x ²– 9, dapat difaktorkan menjadi (x + 3)(x – 3).

Pemfaktoran Kelompok

Pemfaktoran kelompok digunakan untuk memfaktorkan bentuk aljabar yang memiliki empat suku atau lebih. Bentuk ini dapat difaktorkan menjadi dua kelompok, masing-masing terdiri dari dua suku. Jika setiap kelompok memiliki FPB, maka bentuk aljabar tersebut dapat difaktorkan menggunakan FPB tersebut. Misalnya, untuk memfaktorkan x ³+ 2x ²– 3x – 6, dapat difaktorkan menjadi (x ²+ 2x)(x – 3).

Menentukan Hasil Bagi Bentuk Aljabar

Dalam aljabar, menentukan hasil bagi dari dua bentuk aljabar merupakan operasi penting yang digunakan untuk menyederhanakan ekspresi dan menyelesaikan persamaan. Artikel ini akan membahas langkah-langkah menentukan hasil bagi bentuk aljabar dan memberikan contoh untuk memperjelas konsep ini.

Langkah-langkah Menentukan Hasil Bagi Bentuk Aljabar

1. Atur bentuk aljabar dalam bentuk polinomial, dengan suku-suku disusun berdasarkan pangkat yang menurun.
2. Bagi koefisien suku dengan pangkat tertinggi pada pembilang dengan koefisien suku dengan pangkat tertinggi pada penyebut.
3. Turunkan suku hasil bagi yang diperoleh ke bawah pembilang dan kalikan dengan penyebut.
4. Kurangkan hasil perkalian dari pembilang dan turunkan suku berikutnya.
5. Ulangi langkah 2-4 sampai tidak ada lagi suku yang tersisa pada pembilang.

Contoh Soal, Tentukan hasil bagi bentuk aljabar berikut

Tentukan hasil bagi dari bentuk aljabar berikut:

x³

• 2x ²+ 5x
• 6 / x
• 2

Penyelesaian:

1. Atur bentuk aljabar dalam bentuk polinomial: x³
   • 2x ²+ 5x
   • 6
2. Bagi koefisien suku dengan pangkat tertinggi pada pembilang (1) dengan koefisien suku dengan pangkat tertinggi pada penyebut (1): 1/1 = 1
3. Turunkan suku hasil bagi (x ²) ke bawah pembilang dan kalikan dengan penyebut: x ²(x
   • 2) = x ³
   • 2x ²
4. Kurangkan hasil perkalian dari pembilang: (x ³
   • 2x ²+ 5x
   • 6)
   • (x ³
   • 2x ²) = 5x
   • 6
5. Bagi koefisien suku dengan pangkat tertinggi pada pembilang baru (5) dengan koefisien suku dengan pangkat tertinggi pada penyebut (1): 5/1 = 5
6. Turunkan suku hasil bagi (5) ke bawah pembilang dan kalikan dengan penyebut: 5(x
   • 2) = 5x
   • 10
7. Kurangkan hasil perkalian dari pembilang: (5x
   • 6)
   • (5x
   • 10) = 4

Hasil bagi akhir adalah x ²+ 5 + 4/(x – 2).

Penutupan Akhir

Dengan memahami konsep dan metode yang diuraikan dalam artikel ini, pembaca akan dilengkapi dengan pengetahuan dan keterampilan yang diperlukan untuk menentukan hasil bagi bentuk aljabar secara akurat dan efisien. Penguasaan keterampilan ini sangat penting untuk kesuksesan dalam aljabar dan bidang matematika lainnya.

Daftar Pertanyaan Populer

Apa itu hasil bagi bentuk aljabar?

Hasil bagi bentuk aljabar adalah hasil pembagian satu bentuk aljabar dengan bentuk aljabar lainnya.

Mengapa penting untuk menentukan hasil bagi bentuk aljabar?

Menentukan hasil bagi bentuk aljabar membantu menyederhanakan ekspresi kompleks, menyelesaikan persamaan, dan memahami struktur bentuk aljabar.

Apa saja metode yang dapat digunakan untuk menentukan hasil bagi bentuk aljabar?

Metode yang umum digunakan antara lain pembagian bersusun dan pemfaktoran.