Dalam dunia matematika yang luas, pemangkatan memainkan peran penting sebagai operasi dasar yang menyederhanakan perhitungan dan memperluas jangkauan kita dalam memecahkan masalah yang kompleks. Pemangkatan, yang merupakan pengulangan perkalian bilangan dengan dirinya sendiri, hadir dalam berbagai bentuk, mulai dari bilangan bulat hingga matriks, membuka jalan bagi eksplorasi yang mendalam tentang konsep yang menarik ini.

Perjalanan kita akan dimulai dengan mendefinisikan pemangkatan bilangan bulat dan aturannya, diikuti dengan pemahaman pemangkatan bilangan rasional dan kompleks. Selanjutnya, kita akan mengungkap misteri pemangkatan matriks dan menyelidiki aplikasinya yang luas dalam berbagai bidang.

Pemangkatan Bilangan Bulat

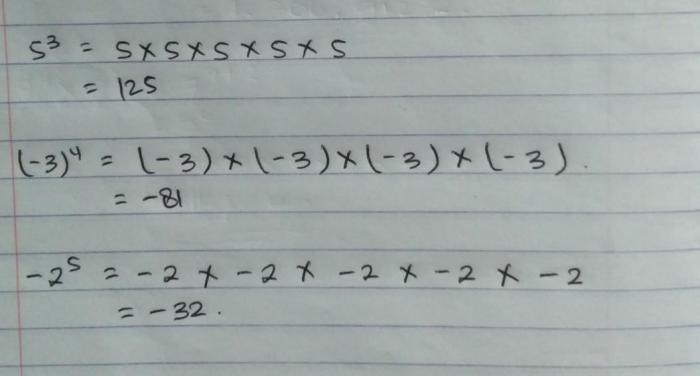
Pemangkatan bilangan bulat merupakan operasi matematika yang melibatkan perkalian berulang dari suatu bilangan dengan dirinya sendiri.

Dalam pemangkatan bilangan bulat, terdapat tiga komponen utama:

• Basis (b): Bilangan yang akan dikalikan dengan dirinya sendiri.
• Eksponen (n): Bilangan yang menunjukkan berapa kali basis dikalikan dengan dirinya sendiri.
• Hasil (bⁿ): Hasil dari perkalian berulang basis.

Contoh Pemangkatan Bilangan Bulat

Sebagai contoh, 3 ⁴ dibaca “tiga pangkat empat” dan berarti 3 x 3 x 3 x 3 = 81.

Aturan Pemangkatan Bilangan Bulat

Terdapat beberapa aturan yang mengatur operasi pemangkatan bilangan bulat:

• Aturan 1: b¹ = b
• Aturan 2: b⁰ = 1 (untuk b ≠ 0)
• Aturan 3: b^m x bⁿ = b^m+n
• Aturan 4: (b^m)ⁿ = b^{m x n}

Pemangkatan Bilangan Rasional

Pemangkatan bilangan rasional melibatkan menaikkan suatu bilangan ke pangkat yang berupa bilangan rasional. Bilangan rasional adalah bilangan yang dapat dinyatakan dalam bentuk p/q, di mana p dan q adalah bilangan bulat dan q tidak sama dengan nol.

Contoh Pemangkatan Bilangan Rasional

Contoh sederhana pemangkatan bilangan rasional adalah 2^(1/2). Ini sama dengan akar kuadrat dari 2, yang merupakan bilangan irasional. Contoh lainnya adalah 3^(-1/3), yang sama dengan 1/akar pangkat tiga dari 3.

Aturan Pemangkatan Bilangan Rasional

Aturan pemangkatan bilangan rasional mengikuti aturan berikut:

• (a^p/q)^r = a^(pr/q)
• (a/b)^p/q = (a^p/q)/(b^p/q)
• a^(-p/q) = 1/(a^p/q)

Pemangkatan Bilangan Kompleks

Pemangkatan bilangan kompleks merupakan operasi matematika yang melibatkan menaikkan bilangan kompleks ke pangkat tertentu. Bilangan kompleks adalah bilangan yang memiliki bagian riil dan bagian imajiner.

Untuk memangkan bilangan kompleks, kita menggunakan aturan berikut:

Konversi ke Bentuk Trigonometri

Konversikan bilangan kompleks ke bentuk trigonometri menggunakan rumus berikut:

• z = r(cos θ + i sin θ)
• di mana r adalah modulus (jarak dari titik asal) dan θ adalah argumen (sudut yang dibentuk oleh bilangan kompleks dengan sumbu x positif).

Pemangkatan

Naikkan modulus ke pangkat yang diberikan:

• rⁿ

Kalikan argumen dengan pangkat yang diberikan:

• nθ

Konversi Kembali ke Bentuk Kartesius

Konversi kembali bilangan kompleks ke bentuk kartesius menggunakan rumus berikut:

• z = rⁿ(cos nθ + i sin nθ)

Contoh

Misalnya, untuk memangkan bilangan kompleks 2 + 3i ke pangkat 2:

• Konversi ke bentuk trigonometri: r = √(2² + 3²) = √13, θ = tan^-1(3/2) ≈ 56,3°
• Pemangkatan: r² = 13, 2θ ≈ 112,6°
• Konversi kembali ke bentuk kartesius: z = 13(cos 112,6° + i sin 112,6°) ≈
  -6,5
  – 8,5i

Pemangkatan Matriks

Pemangkatan matriks adalah operasi yang menaikkan suatu matriks ke pangkat tertentu. Operasi ini berbeda dari pemangkatan bilangan biasa, karena melibatkan perkalian berulang dari matriks itu sendiri.

Konsep Pemangkatan Matriks

Untuk menaikkan matriks A ke pangkat n , kita mengalikan matriks A dengan dirinya sendiri n kali. Hasil perkalian ini disebut A ⁿ , di mana n adalah pangkat.

Contoh Pemangkatan Matriks Sederhana

Misalkan kita memiliki matriks A berikut:

A =

1	2
3	4

Untuk menaikkan matriks A ke pangkat 2, kita mengalikan A dengan dirinya sendiri:

A ² = A x A

1	2
3	4

x

1	2
3	4

=

7	10
15	22

Aturan Pemangkatan Matriks

Terdapat beberapa aturan yang berlaku untuk pemangkatan matriks:

• A¹ = A
• A^m x Aⁿ = A^m+n
• (A^m)ⁿ = A^{m x n}
• (AB)ⁿ = AⁿBⁿ

Aplikasi Pemangkatan

Pemangkatan memiliki aplikasi yang luas dalam berbagai bidang, termasuk matematika, fisika, teknik, dan ekonomi.

Dalam matematika, pemangkatan digunakan untuk:

• Menghitung volume dan luas permukaan bangun ruang.
• Menyelesaikan persamaan polinomial.
• Mempelajari deret geometri dan deret pangkat.

Fisika

Dalam fisika, pemangkatan digunakan untuk:

• Menghitung energi potensial dan energi kinetik.
• Menganalisis gerak benda dalam medan gravitasi.
• Menghitung besaran fisika seperti kecepatan, percepatan, dan gaya.

Teknik

Dalam teknik, pemangkatan digunakan untuk:

• Mendesain struktur dan mesin.
• Menganalisis aliran fluida dan perpindahan panas.
• Menghitung tegangan dan regangan pada material.

Ekonomi

Dalam ekonomi, pemangkatan digunakan untuk:

• Menganalisis pertumbuhan ekonomi.
• Memprediksi nilai investasi.
• Mempelajari inflasi dan suku bunga.

Tantangan dan Solusi Pemangkatan

Pemangkatan adalah operasi matematika yang melibatkan menaikkan suatu bilangan ke pangkat tertentu. Operasi ini banyak digunakan dalam berbagai bidang, seperti matematika, fisika, dan ilmu komputer. Namun, pemangkatan juga dapat menghadirkan tantangan, terutama ketika bilangan yang terlibat sangat besar atau pangkatnya tinggi.

Tantangan

• Ketidakstabilan Numerik: Ketika bilangan yang dipangkatkan sangat besar atau pangkatnya tinggi, perhitungan dapat menjadi tidak stabil, menghasilkan hasil yang tidak akurat atau bahkan tak terhingga.
• Waktu Komputasi yang Lama: Pemangkatan langsung dapat memakan waktu yang sangat lama untuk bilangan yang sangat besar atau pangkat yang tinggi, terutama pada komputer dengan sumber daya terbatas.

Solusi

• Algoritma Pemangkatan Cepat: Algoritma ini menggunakan teknik seperti pengurangan modulus dan penggandaan berulang untuk mengurangi waktu komputasi secara signifikan.
• Perkiraan Pemangkatan: Dalam beberapa kasus, pendekatan perkiraan dapat digunakan untuk memperkirakan hasil pemangkatan dengan tingkat akurasi yang dapat diterima.
• Perangkat Keras Khusus: Komputer dengan perangkat keras khusus, seperti prosesor grafis (GPU), dapat mempercepat perhitungan pemangkatan.

Tips dan Trik

• Gunakan algoritma pemangkatan cepat untuk mengurangi waktu komputasi.
• Pertimbangkan pendekatan perkiraan untuk bilangan yang sangat besar atau pangkat yang tinggi.
• Bagi masalah menjadi bagian-bagian yang lebih kecil untuk memudahkan perhitungan.
• Gunakan kalkulator atau perangkat lunak yang dirancang khusus untuk menangani pemangkatan.

Alat dan Sumber Daya Pemangkatan

Pemangkatan merupakan operasi matematika yang sering digunakan dalam berbagai bidang ilmu. Terdapat beragam alat dan sumber daya yang dapat membantu memudahkan proses pemangkatan.

Kalkulator Online

Kalkulator online seperti Wolfram Alpha dan Symbolab menyediakan fungsi pemangkatan yang mudah digunakan. Alat ini memungkinkan pengguna memasukkan basis dan eksponen untuk menghitung hasil pemangkatan dengan cepat dan akurat.

Aplikasi Perangkat Seluler

Aplikasi perangkat seluler seperti Mathway dan PhotoMath menawarkan fitur pemangkatan yang nyaman. Aplikasi ini memungkinkan pengguna memindai soal matematika dan mendapatkan solusi langkah demi langkah, termasuk perhitungan pemangkatan.

Lembar Kerja Excel

Microsoft Excel menyediakan fungsi POWER() untuk melakukan pemangkatan. Fungsi ini dapat digunakan dalam rumus untuk menghitung hasil pemangkatan secara otomatis. Selain itu, Excel juga menawarkan alat grafik untuk memvisualisasikan hasil pemangkatan.

Tabel Pemangkatan

Tabel pemangkatan memberikan daftar nilai hasil pemangkatan untuk basis dan eksponen tertentu. Tabel ini dapat digunakan sebagai referensi cepat untuk nilai pemangkatan yang umum digunakan.

Rumus dan Identitas Pemangkatan

Memahami rumus dan identitas pemangkatan, seperti a ^m – a ⁿ = a ^m+n dan (a ^m ) ⁿ = a ^mn , sangat membantu dalam menyelesaikan masalah pemangkatan.

Tips Menggunakan Alat Pemangkatan

• Pilih alat yang sesuai dengan kebutuhan Anda, baik untuk perhitungan sederhana atau masalah yang lebih kompleks.
• Verifikasi hasil pemangkatan menggunakan metode lain untuk memastikan akurasi.
• Manfaatkan fitur tambahan seperti grafik dan solusi langkah demi langkah untuk meningkatkan pemahaman.

Pemangkatan dalam Dunia Nyata

Pemangkatan adalah operasi matematika yang memiliki banyak aplikasi dalam kehidupan nyata. Salah satu contohnya adalah dalam bidang keuangan, di mana pemangkatan digunakan untuk menghitung bunga majemuk.

Eksperimen Bunga Majemuk

Tujuan: Mendemonstrasikan konsep bunga majemuk menggunakan pemangkatan.Langkah-langkah:

• Tentukan pokok awal, suku bunga, dan jangka waktu investasi.
• Hitung bunga untuk setiap periode waktu (misalnya, setiap tahun) menggunakan rumus bunga sederhana: Bunga = Pokok x Suku Bunga x Waktu.
• Tambahkan bunga yang diperoleh ke pokok awal untuk mendapatkan pokok baru untuk periode berikutnya.
• Ulangi langkah 2 dan 3 untuk setiap periode waktu.

Hasil:Eksperimen ini menunjukkan bahwa bunga majemuk menyebabkan peningkatan pokok yang lebih cepat dibandingkan bunga sederhana. Hal ini disebabkan oleh fakta bahwa bunga yang diperoleh pada periode sebelumnya juga menghasilkan bunga pada periode berikutnya.Implikasi:Eksperimen ini menyoroti pentingnya pemangkatan dalam menghitung bunga majemuk, yang memiliki implikasi signifikan dalam perencanaan keuangan dan investasi.

Dengan memahami konsep ini, individu dapat membuat keputusan investasi yang lebih tepat dan mengoptimalkan pengembalian mereka.

Ringkasan Terakhir

Pemangkatan, dengan berbagai bentuk dan aplikasinya, merupakan alat yang sangat diperlukan dalam gudang matematika. Dengan memahami konsep dasarnya, kita dapat menaklukkan tantangan dalam menyelesaikan masalah yang kompleks dan memanfaatkan kekuatan pemangkatan untuk mengungkap wawasan baru dalam dunia matematika dan seterusnya.

Pertanyaan dan Jawaban

Apa itu pemangkatan?

Pemangkatan adalah operasi matematika yang melibatkan pengulangan perkalian suatu bilangan dengan dirinya sendiri sejumlah tertentu.

Bagaimana cara menghitung pemangkatan bilangan bulat?

Untuk menghitung pemangkatan bilangan bulat, kita mengalikan bilangan tersebut dengan dirinya sendiri sebanyak pangkat yang diberikan.

Apa saja aplikasi pemangkatan dalam kehidupan nyata?

Pemangkatan memiliki aplikasi yang luas, termasuk perhitungan bunga majemuk, pertumbuhan populasi, dan pemodelan fenomena fisik.