Dalam dunia matematika, matriks memainkan peran penting dalam berbagai aplikasi, mulai dari menyelesaikan sistem persamaan hingga memecahkan masalah geometri. Konsep invers matriks sangat penting untuk memahami sifat dan manipulasi matriks.

Invers matriks, jika ada, adalah matriks yang ketika dikalikan dengan matriks asli menghasilkan matriks identitas. Menentukan invers matriks merupakan operasi fundamental yang memiliki banyak aplikasi praktis, seperti menyelesaikan sistem persamaan linear dan mencari invers fungsi linier.

Pengertian Invers Matriks

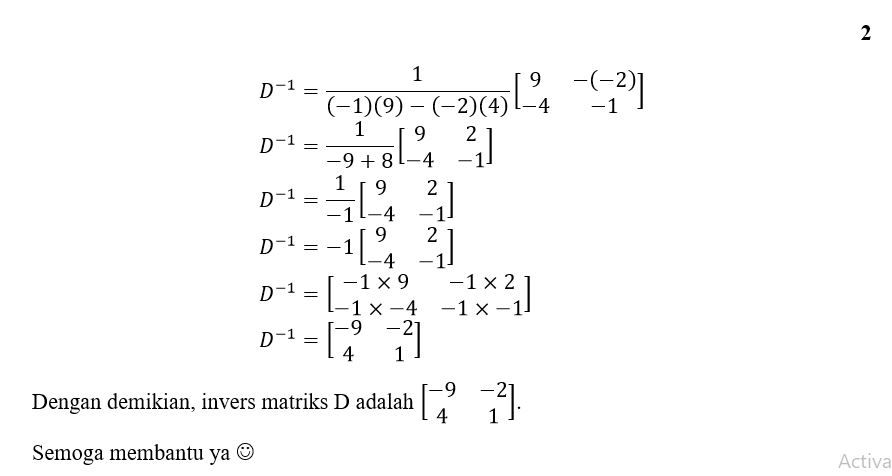
Invers matriks adalah matriks yang ketika dikalikan dengan matriks asli menghasilkan matriks identitas. Matriks identitas adalah matriks persegi yang memiliki 1 pada diagonal utamanya dan 0 pada semua elemen lainnya.

Tidak semua matriks dapat diinvers. Matriks yang dapat diinvers harus memenuhi syarat berikut:

• Matriks harus persegi (jumlah baris sama dengan jumlah kolom).
• Determinan matriks tidak boleh nol.

Jika matriks memenuhi syarat tersebut, maka inversnya dapat ditemukan menggunakan rumus:

A ^-1 = (1/det(A))

C ^T

di mana:* A ^-1 adalah invers matriks A

• det(A) adalah determinan matriks A
• C^T adalah transpose kofaktor matriks A

Metode Menentukan Invers Matriks

Invers matriks merupakan matriks yang ketika dikalikan dengan matriks asli menghasilkan matriks identitas. Menentukan invers matriks sangat penting dalam berbagai aplikasi, seperti menyelesaikan sistem persamaan linear dan mencari determinan. Terdapat dua metode umum untuk menentukan invers matriks: metode kofaktor dan metode Gauss-Jordan.

Metode Kofaktor

Metode kofaktor melibatkan pembuatan tabel kofaktor, di mana setiap elemen adalah determinan dari submatriks yang diperoleh dengan menghapus baris dan kolom elemen tersebut. Tabel kofaktor kemudian ditranspos dan setiap elemennya dibagi dengan determinan matriks asli. Hasilnya adalah invers matriks.

Metode Gauss-Jordan

Metode Gauss-Jordan menggunakan operasi baris dasar untuk mengubah matriks menjadi matriks identitas. Operasi baris dasar ini meliputi menukar baris, mengalikan baris dengan skalar, dan menambahkan baris yang satu dengan baris lainnya. Matriks yang berada di sebelah kanan tanda sama dengan setelah operasi baris dasar selesai adalah invers matriks asli.

Contoh Menentukan Invers Matriks

Invers matriks adalah matriks yang ketika dikalikan dengan matriks asli akan menghasilkan matriks identitas. Menentukan invers matriks sangat penting dalam berbagai bidang, seperti menyelesaikan sistem persamaan linier dan mencari matriks transformasi.

Menggunakan Metode Kofaktor

Metode kofaktor melibatkan menghitung kofaktor untuk setiap elemen matriks, lalu mentranspos tabel kofaktor dan membagi setiap elemen dengan determinan matriks asli.

Menggunakan Metode Gauss-Jordan

Metode Gauss-Jordan melibatkan mengubah matriks menjadi matriks identitas menggunakan operasi baris dasar. Matriks yang berada di sebelah kanan tanda sama dengan adalah invers matriks asli.

Aplikasi Invers Matriks

Invers matriks memiliki berbagai aplikasi penting dalam bidang matematika dan ilmu pengetahuan. Beberapa aplikasi utamanya meliputi:

Menentukan Solusi Sistem Persamaan Linear

Invers matriks dapat digunakan untuk menentukan solusi sistem persamaan linear. Jika kita memiliki sistem persamaan linear yang direpresentasikan sebagai Ax = b , di mana A adalah matriks koefisien, x adalah vektor variabel, dan b adalah vektor konstanta, maka solusi sistem tersebut dapat ditemukan dengan menghitung x = A ^-1 b , di mana A ^-1 adalah invers dari matriks A .

Mencari Invers Fungsi Linier

Invers matriks juga dapat digunakan untuk mencari invers fungsi linier. Jika kita memiliki fungsi linier yang direpresentasikan sebagai y = Ax , maka invers fungsi tersebut dapat ditemukan dengan menghitung x = A ^-1 y .

Memecahkan Masalah Geometri

Invers matriks juga dapat digunakan untuk memecahkan masalah geometri. Misalnya, invers matriks dapat digunakan untuk mencari persamaan garis yang melalui dua titik, menentukan sudut antara dua garis, atau menghitung luas segitiga.

Ringkasan Akhir

Dengan memahami metode penentuan invers matriks, kita dapat memecahkan berbagai masalah matematika dan rekayasa. Invers matriks memberikan alat yang ampuh untuk memanipulasi dan menyelesaikan sistem matriks, sehingga memperluas kemampuan kita untuk menganalisis dan menyelesaikan masalah dunia nyata.

Pertanyaan Umum yang Sering Muncul

Apa syarat suatu matriks dapat diinvers?

Matriks dapat diinvers jika determinannya tidak sama dengan nol.

Apakah semua matriks dapat diinvers?

Tidak, hanya matriks persegi yang determinannya tidak nol yang dapat diinvers.

Apa kegunaan invers matriks dalam kehidupan nyata?

Invers matriks digunakan dalam berbagai aplikasi, seperti analisis sirkuit, desain grafis, dan statistik.