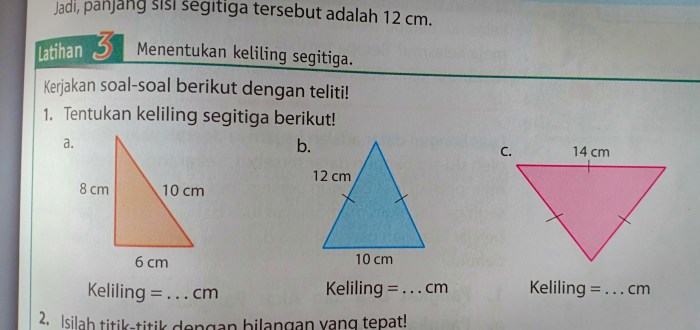
Tentukan keliling dan luas bangun berikut – Dalam dunia geometri, memahami cara menentukan keliling dan luas bangun datar sangat penting. Artikel ini akan mengupas tuntas berbagai jenis bangun datar, rumus keliling dan luasnya, serta contoh soal beserta aplikasi praktisnya dalam kehidupan sehari-hari.
Dengan memahami konsep-konsep dasar ini, kita dapat menyelesaikan masalah geometri secara efektif dan memahami berbagai bentuk dan ukuran yang kita temui di sekitar kita.
Jenis-jenis Bangun Datar
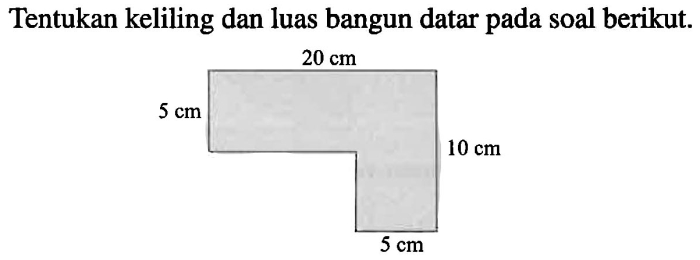
Bangun datar adalah suatu bangun dua dimensi yang memiliki luas dan dibatasi oleh garis-garis lurus atau lengkung. Bangun datar dapat dibagi menjadi beberapa jenis, antara lain:
Segitiga
Segitiga adalah bangun datar yang memiliki tiga sisi dan tiga sudut. Segitiga diklasifikasikan berdasarkan panjang sisinya:
- Segitiga sama sisi: ketiga sisinya sama panjang.
- Segitiga sama kaki: dua sisinya sama panjang.
- Segitiga sembarang: ketiga sisinya tidak sama panjang.
Segiempat
Segiempat adalah bangun datar yang memiliki empat sisi dan empat sudut. Segiempat dapat dibagi menjadi beberapa jenis, antara lain:
- Layang-layang: memiliki dua pasang sisi yang sama panjang, tetapi tidak sejajar.
- Trapesium: memiliki satu pasang sisi sejajar.
- Jajar genjang: memiliki dua pasang sisi sejajar.
- Persegi: memiliki empat sisi yang sama panjang dan empat sudut yang sama besar.
- Persegi panjang: memiliki empat sisi yang sama panjang, tetapi dua pasang sisinya tidak sejajar.
Lingkaran
Lingkaran adalah bangun datar yang dibatasi oleh kurva tertutup yang berjarak sama dari sebuah titik yang disebut pusat.
Elips
Elips adalah bangun datar yang dibatasi oleh kurva tertutup yang menyerupai lingkaran yang memanjang ke satu arah.
Paralelogram, Tentukan keliling dan luas bangun berikut
Paralelogram adalah bangun datar yang memiliki dua pasang sisi sejajar.
Dalam konteks geometri, menghitung keliling dan luas bangun merupakan aspek penting. Proses ini melibatkan penerapan rumus dan pengukuran yang tepat untuk menentukan dimensi bangun. Di sisi lain, dalam kimia, penyetaraan persamaan reaksi redoks ( setarakan persamaan reaksi redoks berikut ) adalah prosedur krusial untuk memahami reaksi kimia.
Sama halnya dengan geometri, penyetaraan persamaan redoks memerlukan pemahaman tentang prinsip-prinsip kimia untuk menyeimbangkan reaksi secara akurat. Dengan menguasai kedua konsep ini, seseorang dapat mengembangkan pemahaman yang komprehensif tentang sifat bangun dan reaksi kimia.
Trapesium Siku-siku
Trapesium siku-siku adalah trapesium yang memiliki salah satu sudutnya siku-siku.
Menentukan keliling dan luas bangun datar merupakan keterampilan dasar dalam geometri. Dalam berbagai aspek kehidupan, seperti arsitektur dan desain interior, perhitungan ini sangat penting. Misalnya, tata ruang rapat harus disesuaikan dengan kapasitas peserta dan kebutuhan kegiatan. Dengan memahami konsep keliling dan luas, kita dapat mengoptimalkan penggunaan ruang dan memastikan kenyamanan bagi semua pihak yang terlibat.
Oleh karena itu, kemampuan menentukan keliling dan luas bangun datar menjadi keterampilan yang esensial dalam berbagai bidang.
Deltoid
Deltoid adalah bangun datar yang memiliki empat sisi yang sama panjang, tetapi tidak sejajar.
Rumus Keliling Bangun Datar: Tentukan Keliling Dan Luas Bangun Berikut
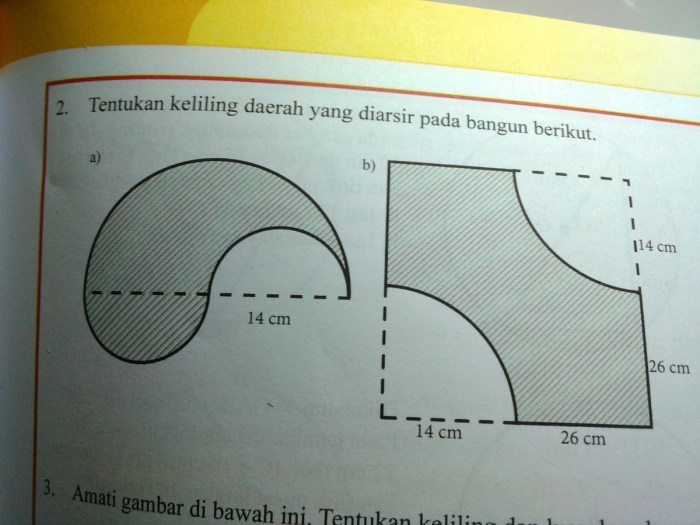
Keliling bangun datar adalah jarak mengelilingi suatu bangun. Keliling dihitung dengan menjumlahkan panjang semua sisi bangun tersebut.
Rumus Keliling Berbagai Bangun Datar
- Persegi: K = 4s
- Persegi panjang: K = 2(p + l)
- Segitiga: K = a + b + c
- Lingkaran: K = 2πr
- Trapesium: K = a + b + c + d
Cara Menggunakan Rumus Keliling
Untuk menggunakan rumus keliling, substitusikan nilai panjang sisi atau jari-jari bangun ke dalam rumus yang sesuai. Misalnya, untuk mencari keliling persegi dengan sisi 5 cm, gunakan rumus K = 4s, di mana s = 5 cm. Maka, K = 4(5 cm) = 20 cm.
Rumus Luas Bangun Datar

Rumus luas bangun datar digunakan untuk menentukan ukuran area permukaan dua dimensi. Berbagai bentuk bangun datar memiliki rumus luas yang berbeda-beda.
Berikut adalah tabel yang merangkum rumus luas untuk berbagai bangun datar:
| Bangun Datar | Rumus Luas |
|---|---|
| Persegi | sisi2 |
| Persegi Panjang | panjang x lebar |
| Segitiga | 1/2 x alas x tinggi |
| Lingkaran | πr2 |
| Jajar Genjang | alas x tinggi |
| Trapesium | 1/2 x (alas1 + alas2) x tinggi |
| Layang-layang | 1/2 x diagonal1 x diagonal2 |
Untuk menggunakan rumus luas, substitusikan nilai yang diketahui ke dalam rumus dan hitung hasilnya. Misalnya, untuk menghitung luas persegi panjang dengan panjang 5 cm dan lebar 3 cm, kita substitusikan nilai-nilai tersebut ke dalam rumus luas persegi panjang: Luas = panjang x lebar = 5 cm x 3 cm = 15 cm 2.
Menentukan keliling dan luas bangun datar merupakan kompetensi dasar yang diujikan dalam soal essay seni budaya kelas 7 semester 1 . Kemampuan ini penting untuk memahami konsep dasar geometri dan mengaplikasikannya dalam kehidupan sehari-hari. Dengan menguasai teknik penentuan keliling dan luas bangun, siswa dapat menyelesaikan berbagai soal terkait pengukuran dan perhitungan geometri.
Contoh Soal Keliling dan Luas Bangun Datar

Keliling dan luas bangun datar merupakan konsep dasar geometri yang penting untuk dipahami. Berikut ini beberapa contoh soal yang dapat membantu memahami konsep tersebut.
Persegi
- Sebuah persegi memiliki panjang sisi 5 cm. Tentukan keliling dan luas persegi tersebut.
- Sebuah persegi memiliki keliling 20 cm. Tentukan panjang sisi dan luas persegi tersebut.
Persegi Panjang
- Sebuah persegi panjang memiliki panjang 10 cm dan lebar 5 cm. Tentukan keliling dan luas persegi panjang tersebut.
- Sebuah persegi panjang memiliki keliling 30 cm dan panjang 10 cm. Tentukan lebar dan luas persegi panjang tersebut.
Segitiga
- Sebuah segitiga siku-siku memiliki panjang sisi miring 10 cm dan salah satu sisi lainnya 6 cm. Tentukan keliling dan luas segitiga tersebut.
- Sebuah segitiga sama sisi memiliki panjang sisi 8 cm. Tentukan keliling dan luas segitiga tersebut.
Lingkaran
- Sebuah lingkaran memiliki jari-jari 7 cm. Tentukan keliling dan luas lingkaran tersebut.
- Sebuah lingkaran memiliki keliling 44 cm. Tentukan jari-jari dan luas lingkaran tersebut.
Aplikasi Keliling dan Luas Bangun Datar

Keliling dan luas bangun datar memiliki banyak aplikasi praktis dalam kehidupan sehari-hari, terutama dalam bidang konstruksi, desain, dan perencanaan.
Konstruksi
Dalam konstruksi, keliling dan luas digunakan untuk menghitung bahan yang dibutuhkan, seperti panjang kayu untuk membangun dinding atau luas permukaan yang perlu dicat. Mengetahui keliling dan luas memungkinkan kontraktor merencanakan dan memperkirakan biaya proyek secara akurat.
Desain
Di bidang desain, keliling dan luas digunakan untuk menentukan proporsi dan skala objek. Arsitek menggunakannya untuk merencanakan denah lantai dan desain interior, sementara desainer grafis menggunakannya untuk membuat logo dan materi pemasaran.
Perencanaan
Keliling dan luas juga penting dalam perencanaan. Perencana kota menggunakannya untuk menentukan tata letak jalan dan area hijau, sementara insinyur sipil menggunakannya untuk merancang jembatan dan sistem irigasi. Mengetahui keliling dan luas memungkinkan perencana mengoptimalkan penggunaan ruang dan sumber daya.
Contoh Lainnya
- Menghitung luas tanah untuk menentukan nilai properti
- Merencanakan tata letak furnitur di sebuah ruangan
- Menentukan jumlah ubin yang dibutuhkan untuk menutupi lantai
- Menghitung luas permukaan benda untuk menentukan volume
- Merencanakan area tanam untuk pertanian
Ringkasan Penutup

Menguasai cara menentukan keliling dan luas bangun datar tidak hanya memperkaya pengetahuan matematika kita, tetapi juga membekali kita dengan keterampilan penting untuk berbagai bidang, mulai dari konstruksi hingga desain. Dengan memahami konsep-konsep ini, kita dapat mengukur, merencanakan, dan membangun dengan lebih akurat dan efisien.
FAQ Lengkap
Apa itu keliling bangun datar?
Keliling bangun datar adalah jarak total di sekitar tepinya.
Apa itu luas bangun datar?
Luas bangun datar adalah ukuran besar kecilnya permukaan bangun tersebut.