Tentukan persamaan garis singgung lingkaran – Persamaan garis singgung lingkaran merupakan alat penting dalam matematika dan fisika. Artikel ini akan memberikan panduan langkah demi langkah untuk menentukan persamaan garis singgung lingkaran, lengkap dengan contoh soal dan penerapan praktisnya.

Persamaan garis singgung lingkaran menggambarkan garis yang bersinggungan dengan lingkaran pada satu titik, yang dikenal sebagai titik singgung. Garis singgung ini memiliki sifat unik yang menjadikannya sangat berguna dalam berbagai aplikasi.

Pengertian Persamaan Garis Singgung Lingkaran: Tentukan Persamaan Garis Singgung Lingkaran

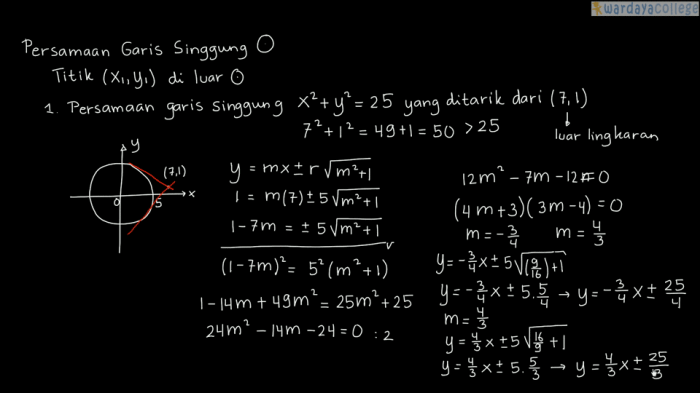
Persamaan garis singgung lingkaran adalah persamaan yang menyatakan hubungan antara titik singgung dan garis singgung yang ditarik dari titik tersebut terhadap lingkaran.

Garis singgung adalah garis lurus yang bersinggungan dengan lingkaran pada satu titik saja, yang disebut titik singgung.

Syarat-syarat Garis Singgung Lingkaran

• Garis singgung tegak lurus dengan jari-jari lingkaran yang ditarik ke titik singgung.
• Persamaan garis singgung lingkaran dapat dinyatakan dalam bentuk persamaan garis lurus, yaitu y = mx + c.
• Nilai kemiringan garis singgung (m) sama dengan invers dari nilai kemiringan jari-jari yang ditarik ke titik singgung.
• Nilai titik potong garis singgung dengan sumbu y (c) dapat dicari dengan mensubstitusikan titik singgung ke persamaan garis singgung.

Cara Menentukan Persamaan Garis Singgung Lingkaran

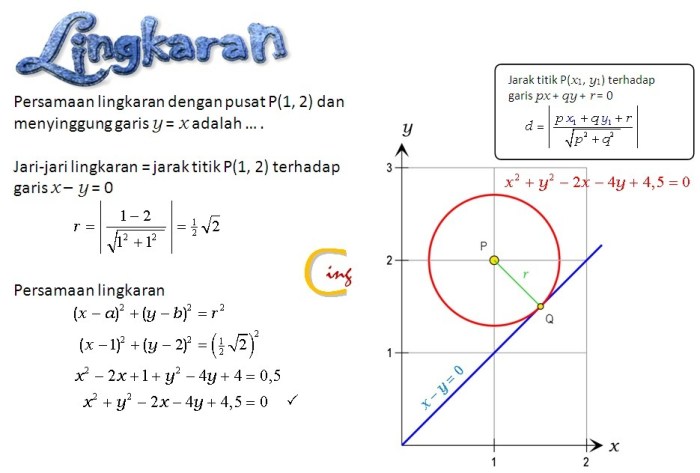
Dalam geometri, garis singgung lingkaran adalah garis lurus yang menyentuh lingkaran pada satu titik. Persamaan garis singgung dapat ditentukan menggunakan rumus matematika tertentu.

Langkah-langkah Menentukan Persamaan Garis Singgung Lingkaran

• Tentukan titik singgung lingkaran (T).
• Tarik garis lurus melalui titik singgung yang tegak lurus dengan jari-jari yang menghubungkan titik singgung dengan pusat lingkaran.
• Tentukan kemiringan garis singgung (m) dengan rumus: m = -1 / (kemiringan jari-jari).
• Gunakan persamaan garis lurus (y = mx + c) dengan titik T dan kemiringan m untuk menentukan persamaan garis singgung.

Rumus Persamaan Garis Singgung Lingkaran, Tentukan persamaan garis singgung lingkaran

Persamaan Garis Singgung Lingkaran: y

Dalam menentukan persamaan garis singgung lingkaran, salah satu caranya adalah dengan menggunakan konsep gradien. Gradien ini dapat diperoleh dari persamaan umum garis, yaitu y = mx + c. Dengan memperhatikan persamaan lingkaran, x^2 + y^2 = r^2, kita dapat menentukan gradien garis singgung dengan mengambil turunan implisit terhadap x dan menggantikan nilai x pada titik singgung.

Penentuan titik singgung ini dapat dilakukan dengan menyelesaikan sistem persamaan yang melibatkan persamaan lingkaran dan persamaan garis. Seperti dalam lagu look at the butterfly it beautiful colours , keindahan dapat ditemukan dalam hal-hal kecil, seperti menentukan persamaan garis singgung lingkaran yang melibatkan perhitungan matematis yang cermat.

• y_T= (x
• x _T) / (-1 / m)

di mana:

• (x _T, y _T) adalah koordinat titik singgung
• m adalah kemiringan garis singgung

Contoh Penentuan Persamaan Garis Singgung Lingkaran

Misalkan kita memiliki lingkaran dengan pusat di titik (2, 3) dan jari-jari 5. Jika garis singgung lingkaran melalui titik (7, 5), maka persamaan garis singgungnya adalah:

1. Tentukan titik singgung T. Karena garis singgung tegak lurus dengan jari-jari, maka T terletak pada garis lurus yang menghubungkan titik (7, 5) dan (2, 3).
2. Tentukan kemiringan jari-jari: m_r= (5
   • 3) / (7
   • 2) = 2/5
3. Tentukan kemiringan garis singgung: m =
   • 1 / m _r=
   • 5/2
4. Substitusikan titik T dan m ke dalam persamaan garis singgung: y
   • 5 = (x
   • 7) / (-5/2)
5. Sederhanakan persamaan: 2(y
   • 5) =
   • (x
   • 7)
6. Persamaan garis singgung lingkaran: 2y
   • 10 =
   • x + 7 atau x + 2y = 17

Contoh Menentukan Persamaan Garis Singgung Lingkaran

Untuk menentukan persamaan garis singgung lingkaran, diperlukan titik singgung dan gradien garis singgung. Berikut langkah-langkahnya:

Titik Singgung

Titik singgung adalah titik di mana garis singgung menyinggung lingkaran. Untuk menentukan titik singgung, gunakan persamaan lingkaran:

x²+ y ²= r ²

di mana (x, y) adalah koordinat titik singgung dan r adalah jari-jari lingkaran.

Dalam matematika, menentukan persamaan garis singgung lingkaran memerlukan pemahaman tentang geometri analitik. Di sisi lain, Indonesia memiliki kekayaan sumber daya alam, termasuk sungai-sungai yang melimpah. Seperti Sungai Musi yang berasal dari Sumatra Selatan atau Sungai Kapuas yang berhulu di Kalimantan Barat ( nama sungai di indonesia dan asal daerahnya ). Mengetahui asal-usul sungai ini dapat membantu kita memahami hidrologi Indonesia.

Demikian pula, memahami persamaan garis singgung lingkaran sangat penting dalam berbagai aplikasi matematika, seperti kalkulus dan trigonometri.

Gradien Garis Singgung

Gradien garis singgung tegak lurus dengan jari-jari lingkaran yang melalui titik singgung. Oleh karena itu, gradien garis singgung adalah:

m =

1/m_r

di mana m adalah gradien garis singgung dan m _radalah gradien jari-jari lingkaran.

Persamaan Garis Singgung

Persamaan garis singgung dapat ditentukan menggunakan persamaan titik-gradien:

y

• y₁= m(x
• x ₁)

di mana (x ₁, y ₁) adalah koordinat titik singgung dan m adalah gradien garis singgung.

Dalam matematika, menentukan persamaan garis singgung lingkaran merupakan konsep penting yang dibahas dalam materi bahasa Indonesia kelas XI semester 2 . Dengan memahami konsep ini, siswa dapat mengidentifikasi garis yang bersinggungan dengan lingkaran dan menentukan persamaannya. Kemampuan ini sangat berguna dalam berbagai aplikasi, seperti dalam geometri dan kalkulus.

Penerapan Persamaan Garis Singgung Lingkaran

Persamaan garis singgung lingkaran memiliki berbagai aplikasi dalam berbagai bidang, seperti geometri, fisika, dan teknik. Persamaan ini memungkinkan kita untuk menentukan garis lurus yang bersinggungan dengan lingkaran pada satu titik.

Geometri

• Mencari titik singgung dua lingkaran
• Menentukan garis singgung suatu lingkaran yang melalui titik tertentu di luar lingkaran
• Membagi garis lurus menjadi dua bagian sama panjang oleh lingkaran

Fisika

• Menghitung lintasan proyektil yang mengenai permukaan melengkung
• Menentukan titik pantul sinar cahaya pada cermin parabola
• Menganalisis pergerakan benda pada bidang lengkung

Teknik

• Merancang roda gigi dan puli
• Menganalisis kontak antara permukaan melengkung
• Membuat lintasan untuk kendaraan pada jalan melengkung

Simpulan Akhir

Memahami cara menentukan persamaan garis singgung lingkaran sangat penting untuk berbagai bidang, termasuk geometri, fisika, dan teknik. Persamaan ini memberikan wawasan tentang hubungan antara lingkaran dan garis, memungkinkan kita memecahkan masalah dan membuat prediksi yang akurat.

Sudut Pertanyaan Umum (FAQ)

Apa itu garis singgung lingkaran?

Garis singgung lingkaran adalah garis yang bersinggungan dengan lingkaran pada satu titik, yang dikenal sebagai titik singgung.

Bagaimana cara menentukan titik singgung lingkaran?

Titik singgung lingkaran dapat ditentukan dengan mencari titik perpotongan antara lingkaran dan garis normal pada titik tersebut.

Apa saja penerapan persamaan garis singgung lingkaran?

Persamaan garis singgung lingkaran digunakan dalam berbagai bidang, seperti geometri untuk menghitung jarak antara dua titik, fisika untuk menganalisis gerak benda, dan teknik untuk merancang struktur yang efisien.