Tentukan persamaan garis yang melalui titik – Menentukan persamaan garis yang melalui titik adalah keterampilan penting dalam matematika. Ini memungkinkan kita memodelkan hubungan linier antara dua variabel dan memprediksi nilai yang tidak diketahui. Artikel ini akan memandu Anda melalui langkah-langkah untuk menentukan persamaan garis melalui titik, dilengkapi dengan contoh dan ilustrasi grafis.

Persamaan garis umumnya ditulis dalam bentuk y = mx + c, di mana m adalah kemiringan dan c adalah titik potong y. Dengan mengetahui koordinat titik yang dilalui garis, kita dapat menentukan nilai m dan c dan memperoleh persamaan garis tersebut.

Persamaan Garis

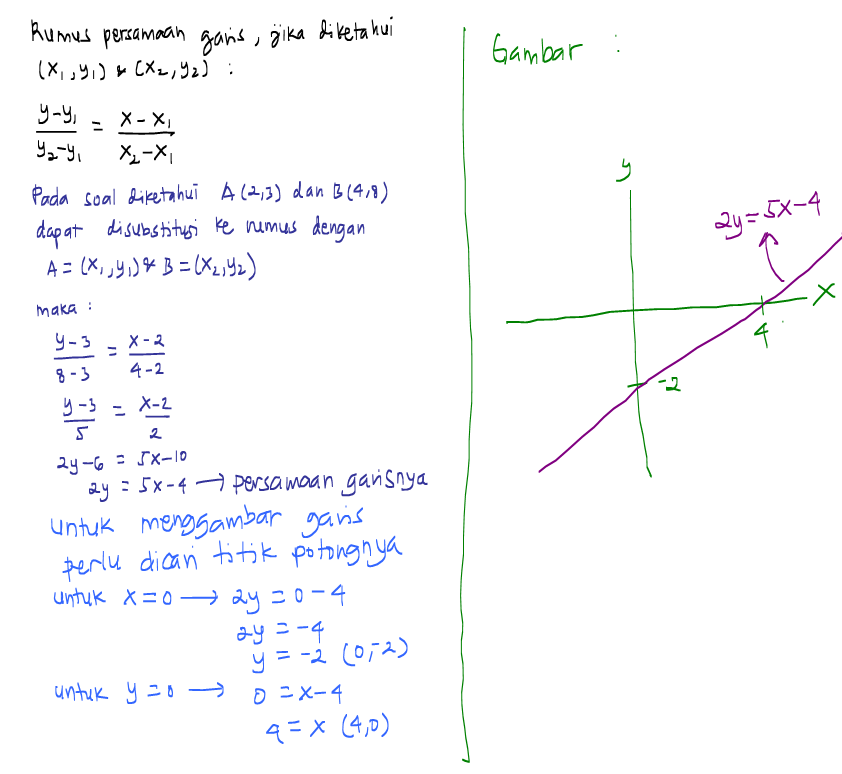
Persamaan garis adalah persamaan matematika yang menggambarkan garis pada bidang koordinat. Persamaan garis dapat digunakan untuk menentukan kemiringan, perpotongan y, dan karakteristik lainnya dari suatu garis.

Bentuk umum persamaan garis adalah y = mx + c, di mana:

• madalah kemiringan garis
• cadalah perpotongan y garis
• xdan yadalah variabel yang mewakili koordinat titik pada garis

Kemiringan Garis

Kemiringan garis adalah ukuran seberapa curam garis tersebut. Kemiringan dihitung dengan membagi selisih nilai ydengan selisih nilai xuntuk dua titik pada garis.

Perpotongan y Garis

Perpotongan y garis adalah titik di mana garis memotong sumbu y. Perpotongan y adalah nilai yketika x= 0.

Bentuk Persamaan Garis Lainnya

Selain bentuk umum y = mx + c, terdapat beberapa bentuk persamaan garis lainnya:

• Bentuk titik-kemiringan: y- y ₁= m(x – x ₁)
• Bentuk dua titik: (y- y ₂)/(x – x ₂) = (y ₁– y ₂)/(x ₁– x ₂)
• Bentuk perpotongan x dan y: x/a + y/b = 1

Bentuk persamaan garis yang digunakan tergantung pada informasi yang diketahui tentang garis tersebut.

Dalam matematika, persamaan garis yang melalui suatu titik dapat ditentukan menggunakan rumus titik-lereng. Rumus ini mengandalkan pemahaman tentang personal computer , yang merupakan perangkat elektronik yang dapat diprogram untuk melakukan berbagai tugas. Kembali ke persamaan garis, setelah mengetahui titik dan kemiringannya, persamaan dapat ditulis dalam bentuk y = mx + b, di mana m adalah kemiringan dan b adalah titik potong y.

Persamaan Garis yang Melalui Titik

Dalam matematika, persamaan garis dapat digunakan untuk menggambarkan garis lurus pada bidang koordinat. Persamaan garis ini ditentukan oleh kemiringan garis dan titik yang dilalui oleh garis tersebut.

Bentuk Umum Persamaan Garis

Bentuk umum persamaan garis adalah y = mx + c, di mana:

• y adalah variabel dependen (ordinat)
• x adalah variabel independen (absis)
• m adalah kemiringan garis
• c adalah titik potong garis dengan sumbu y

Menentukan Persamaan Garis yang Melalui Titik

Untuk menentukan persamaan garis yang melalui titik (x1, y1), kita dapat menggunakan rumus berikut:

y

• y1 = m(x
• x1)

di mana m adalah kemiringan garis dan (x1, y1) adalah titik yang dilalui oleh garis tersebut.

Contoh

Misalkan kita ingin menentukan persamaan garis yang melalui titik (2, 3) dan memiliki kemiringan 2.

Menggunakan rumus di atas, kita dapat memperoleh:

y

• 3 = 2(x
• 2)

y

• 3 = 2x
• 4

y = 2x

1

Jadi, persamaan garis yang melalui titik (2, 3) dan memiliki kemiringan 2 adalah y = 2x- 1 .

Menentukan Persamaan Garis

Persamaan garis adalah persamaan matematika yang mewakili suatu garis lurus pada bidang koordinat. Persamaan ini dapat digunakan untuk menentukan kemiringan, titik potong sumbu y, dan sifat-sifat garis lainnya.

Langkah-Langkah Menentukan Persamaan Garis Melalui Titik, Tentukan persamaan garis yang melalui titik

1. Tentukan dua titik yang terletak pada garis tersebut.
2. Tentukan kemiringan garis menggunakan rumus: $$m = (y_2
   • y_1) / (x_2
   • x_1)$$

   di mana $(x_1, y_1)$ dan $(x_2, y_2)$ adalah koordinat kedua titik.

3. Tentukan titik potong sumbu y menggunakan rumus: $$b = y_1
   

   mx_1$$

   Untuk menentukan persamaan garis yang melalui suatu titik, diperlukan koordinat titik dan kemiringan garis. Kemiringan dapat diperoleh dengan menggunakan rumus the ingredients of the product are mostly , yaitu selisih koordinat y dibagi selisih koordinat x dari dua titik yang berbeda pada garis tersebut.

   Setelah diketahui kemiringan dan titik yang dilalui garis, persamaan garis dapat ditentukan dengan menggunakan bentuk titik-kemiringan, yaitu y = mx + c, di mana m adalah kemiringan dan c adalah titik potong y.

   di mana $(x_1, y_1)$ adalah salah satu titik pada garis dan $m$ adalah kemiringan.

4. Tulis persamaan garis dalam bentuk umum: $$y = mx + b$$

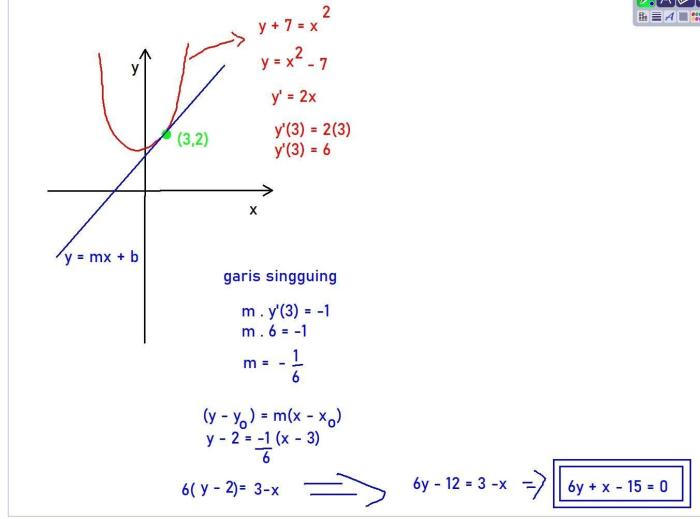
Rumus Persamaan Garis Melalui Titik

Persamaan garis melalui titik $(x_1, y_1)$ dengan kemiringan $m$ dapat ditulis sebagai:$$y

• y_1 = m(x
• x_1)$$

atau dalam bentuk umum:$$y = mx + b$$di mana $b = y_1

mx_1$ adalah titik potong sumbu y.

Persamaan Garis Melalui Titik

Persamaan garis merupakan representasi matematis dari garis lurus pada bidang koordinat. Untuk menentukan persamaan garis yang melalui sebuah titik tertentu, kita memerlukan dua informasi:

• Koordinat titik yang dilalui garis
• Gradien atau kemiringan garis

Menentukan Gradien

Gradien (m) suatu garis adalah nilai yang menyatakan kemiringannya. Ini dihitung dengan membagi perubahan koordinat vertikal (Δy) dengan perubahan koordinat horizontal (Δx) antara dua titik yang terletak pada garis tersebut. Jika koordinat titik yang dilalui garis adalah (x₁, y₁) dan (x₂, y₂), maka gradiennya adalah:

m = (y₂ – y₁) / (x₂ – x₁)

Menentukan Persamaan Garis

Dengan mengetahui gradien dan koordinat titik yang dilalui garis, kita dapat menentukan persamaan garis menggunakan persamaan garis titik-gradien:

y – y₁ = m(x – x₁)

Dimana (x₁, y₁) adalah koordinat titik yang dilalui garis, dan m adalah gradien garis.

Dalam matematika, menentukan persamaan garis yang melalui titik tertentu merupakan konsep dasar. Untuk melatih pemahaman konsep ini, dapat dikerjakan latihan soal matematika kelas 4 semester 1 . Melalui latihan soal tersebut, siswa dapat mengasah kemampuan mereka dalam menentukan persamaan garis yang melalui titik, sekaligus memperkuat pemahaman mereka tentang konsep geometri dasar.

Contoh dan Prosedur: Tentukan Persamaan Garis Yang Melalui Titik

Untuk menentukan persamaan garis melalui titik, dapat dilakukan dengan berbagai cara. Berikut beberapa contoh dan langkah-langkah prosedurnya:

Contoh Persamaan Garis

• Persamaan garis yang melalui titik (2, 5) dan (4, 7): y = x + 3
• Persamaan garis yang melalui titik (-1, 3) dan (3, 1): y = -2/3x + 5/3
• Persamaan garis yang melalui titik (0, 0) dan (2, 4): y = 2x

Langkah-langkah Prosedur

1. Tentukan dua titik yang dilalui garis:Misalkan titik tersebut adalah (x1, y1) dan (x2, y2).
2. Hitung gradien garis:Gradien (m) adalah kemiringan garis dan dihitung menggunakan rumus: m = (y2
   • y1) / (x2
   • x1).
3. Tentukan titik potong sumbu y:Titik potong sumbu y (b) adalah titik di mana garis memotong sumbu y. Ini dapat dihitung menggunakan rumus: b = y1
   

   mx1.

4. Tulis persamaan garis:Persamaan garis dapat ditulis dalam bentuk y = mx + b, di mana m adalah gradien dan b adalah titik potong sumbu y.

Catatan: Jika gradien tidak dapat ditentukan karena kedua titik memiliki nilai x yang sama, maka garis tersebut vertikal dan persamaannya adalah x = nilai x titik tersebut.

Penutupan Akhir

Memahami cara menentukan persamaan garis melalui titik sangat penting untuk berbagai aplikasi, termasuk grafik, analisis data, dan pemodelan. Dengan mengikuti langkah-langkah yang diuraikan dalam artikel ini, Anda dapat dengan mudah menemukan persamaan garis yang mewakili hubungan linier antara dua titik atau lebih.

Pertanyaan Populer dan Jawabannya

Apa itu persamaan garis?

Persamaan garis adalah persamaan matematika yang mewakili garis pada bidang koordinat. Persamaan garis umumnya ditulis dalam bentuk y = mx + c, di mana m adalah kemiringan dan c adalah titik potong y.

Bagaimana menentukan persamaan garis melalui titik?

Untuk menentukan persamaan garis melalui titik, Anda perlu mengetahui koordinat titik yang dilalui garis tersebut. Kemudian, Anda dapat menggunakan rumus persamaan garis melalui titik, y – y1 = m(x – x1), di mana (x1, y1) adalah koordinat titik dan m adalah kemiringan.

Apa itu kemiringan garis?

Kemiringan garis adalah ukuran seberapa curam garis tersebut. Kemiringan dihitung sebagai perubahan y dibagi dengan perubahan x antara dua titik pada garis.