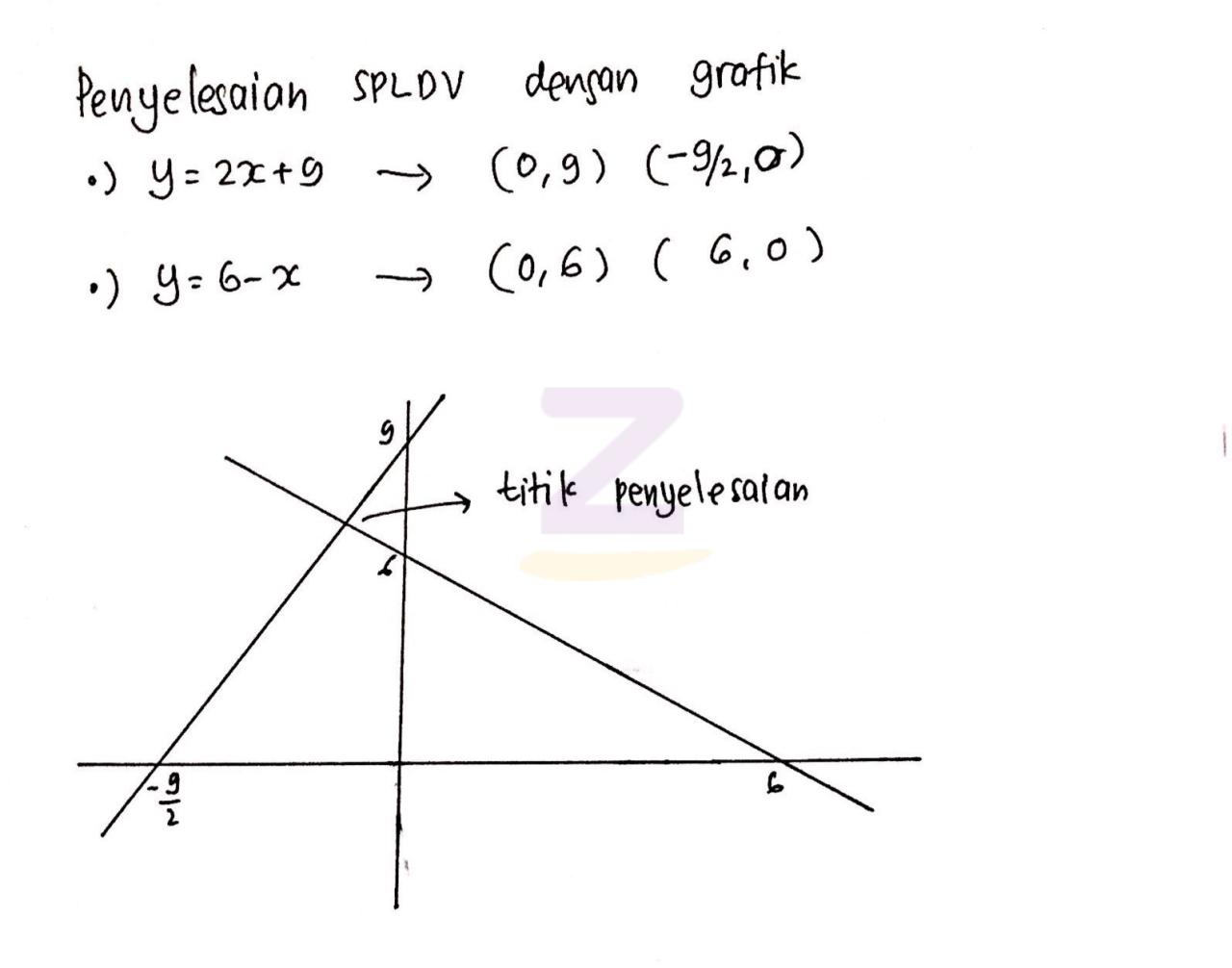
Tentukan selesaian dari persamaan berikut – Penyelesaian persamaan merupakan keterampilan penting dalam matematika yang memiliki berbagai aplikasi dalam berbagai bidang. Artikel ini akan menguraikan jenis-jenis persamaan umum, metode penyelesaian, langkah-langkah sistematis, dan contoh praktis untuk membantu Anda menguasai teknik penting ini.
Persamaan matematika melibatkan variabel yang mewakili nilai yang tidak diketahui, dan tujuannya adalah untuk menemukan nilai tersebut yang memenuhi persamaan.
Persamaan Matematika: Tentukan Selesaian Dari Persamaan Berikut
Persamaan matematika merupakan representasi matematis yang menyatakan kesetaraan antara dua ekspresi aljabar. Persamaan ini memainkan peran penting dalam berbagai bidang, termasuk sains, teknik, ekonomi, dan kehidupan sehari-hari.
Terdapat berbagai jenis persamaan matematika, antara lain:
- Persamaan Linear: Persamaan yang memiliki pangkat tertinggi dari variabel yang tidak diketahui adalah 1.
- Persamaan Kuadrat: Persamaan yang memiliki pangkat tertinggi dari variabel yang tidak diketahui adalah 2.
- Persamaan Kubik: Persamaan yang memiliki pangkat tertinggi dari variabel yang tidak diketahui adalah 3.
Mampu menyelesaikan persamaan matematika sangat penting karena memungkinkan kita untuk:
- Menentukan nilai yang tidak diketahui dari variabel.
- Membuat model dan memprediksi hasil dalam berbagai situasi.
- Menganalisis data dan membuat keputusan yang tepat.
Metode Penyelesaian
Persamaan dapat diselesaikan menggunakan berbagai metode, masing-masing dengan kelebihan dan kekurangannya sendiri. Metode yang umum digunakan antara lain:
Faktorisasi
Faktorisasi melibatkan memecah persamaan menjadi faktor-faktornya. Metode ini efektif untuk persamaan yang dapat difaktorkan dengan mudah, seperti persamaan kuadrat yang memiliki akar rasional.
Melengkapi Kuadrat
Melengkapi kuadrat melibatkan penambahan dan pengurangan suku konstanta tertentu ke kedua sisi persamaan untuk mengubahnya menjadi bentuk kuadrat sempurna. Metode ini berguna untuk persamaan kuadrat yang tidak dapat difaktorkan dengan mudah.
Rumus Kuadrat
Rumus kuadrat adalah formula umum yang dapat digunakan untuk menyelesaikan persamaan kuadrat dalam bentuk ax 2+ bx + c = 0. Metode ini memberikan solusi yang tepat, tetapi dapat lebih rumit daripada metode faktorisasi atau melengkapi kuadrat.
Tabel berikut merangkum kelebihan dan kekurangan dari masing-masing metode ini:
| Metode | Kelebihan | Kekurangan |
|---|---|---|
| Faktorisasi | – Mudah digunakan untuk persamaan yang dapat difaktorkan
|
– Tidak selalu dapat digunakan untuk semua persamaan |
| Melengkapi Kuadrat | – Dapat digunakan untuk persamaan yang tidak dapat difaktorkan
|
– Lebih rumit daripada faktorisasi |
| Rumus Kuadrat | – Dapat digunakan untuk semua persamaan kuadrat
|
– Lebih rumit daripada faktorisasi atau melengkapi kuadrat |
Langkah-langkah Penyelesaian Persamaan
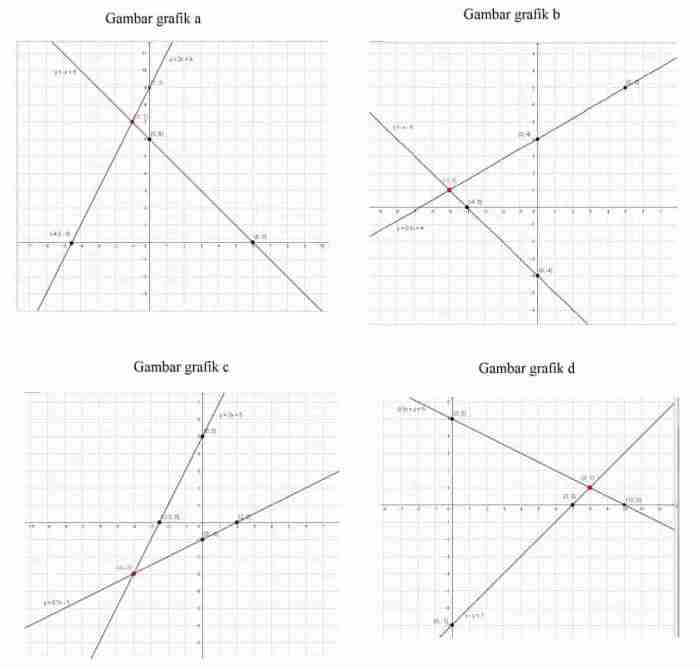
Menyelesaikan persamaan melibatkan langkah-langkah sistematis untuk mengisolasi variabel yang diinginkan dan menemukan nilainya. Langkah-langkah ini meliputi:
Mengisolasi Variabel yang Diinginkan
Pindahkan semua suku yang mengandung variabel yang diinginkan ke satu sisi persamaan, dan semua suku konstan ke sisi lainnya.
Menerapkan Operasi Matematika
Terapkan operasi matematika dasar (penambahan, pengurangan, perkalian, pembagian) ke kedua sisi persamaan untuk menyederhanakannya dan mengisolasi variabel lebih lanjut.
Dalam konteks penentuan selesaian persamaan, perlu dipertimbangkan pula aspek historis. Seperti diketahui, saat masih kecil sunan giri memiliki nama yang berbeda. Hal ini menunjukkan bahwa nama dapat berubah seiring waktu, sama seperti solusi persamaan yang dapat bervariasi tergantung pada parameter yang terlibat.
Oleh karena itu, penting untuk mempertimbangkan konteks dan parameter tertentu saat mencari solusi persamaan, baik dalam matematika maupun dalam bidang lainnya.
Memeriksa Solusi
Setelah menemukan solusi, substitusikan kembali ke persamaan asli untuk memverifikasi apakah persamaan tersebut benar.
Contoh Langkah demi Langkah
Untuk menyelesaikan persamaan 2x + 5 = 15, kita dapat mengikuti langkah-langkah berikut:
- Kurangi 5 dari kedua sisi: 2x = 10
- Bagi kedua sisi dengan 2: x = 5
- Substitusi x = 5 ke persamaan asli untuk memeriksa: 2(5) + 5 = 15 (benar)
Dengan mengikuti langkah-langkah ini secara sistematis, kita dapat menyelesaikan persamaan apa pun dan menemukan nilai variabel yang diinginkan.
Untuk menentukan selesaian dari persamaan berikut, diperlukan pemahaman tentang aljabar. Referensi yang komprehensif tentang topik ini dapat ditemukan dalam materi sejarah indonesia kelas 11 semester 2 pdf, yang tersedia secara online di sini . Dengan mengacu pada sumber ini, individu dapat memperoleh wawasan yang lebih dalam tentang teknik penyelesaian persamaan dan mengembangkan keterampilan analitis yang diperlukan untuk menyelesaikan persamaan dengan sukses.
Penyelesaian Persamaan
Persamaan adalah pernyataan matematika yang menyatakan bahwa dua ekspresi memiliki nilai yang sama. Untuk menyelesaikan persamaan, kita harus menemukan nilai variabel yang membuat kedua sisi persamaan tersebut sama.
Metode Penyelesaian Persamaan
Ada beberapa metode yang dapat digunakan untuk menyelesaikan persamaan, antara lain:
- Menjumlahkan atau mengurangkan bilangan yang sama pada kedua sisi persamaan
- Mengalikan atau membagi kedua sisi persamaan dengan bilangan yang sama (selain 0)
- Menggunakan rumus khusus untuk jenis persamaan tertentu (seperti persamaan kuadrat)
Contoh Penyelesaian Persamaan
Misalkan kita memiliki persamaan berikut:
x + 5 = 10
Untuk menyelesaikan persamaan ini, kita dapat mengurangi 5 dari kedua sisi:
x + 5
- 5 = 10
- 5
x = 5
Jadi, nilai x yang memenuhi persamaan tersebut adalah 5.
Contoh dan Aplikasi
Penyelesaian persamaan memiliki peran penting dalam berbagai bidang kehidupan nyata, termasuk:
Fisika (Gerak Benda)
- Menentukan kecepatan, percepatan, dan posisi benda yang bergerak.
- Memprediksi lintasan peluru atau roket.
Kimia (Kesetimbangan Kimia)
- Menghitung konsentrasi reaktan dan produk dalam reaksi kesetimbangan.
- Memprediksi arah reaksi dan konstanta kesetimbangan.
Ekonomi (Penentuan Titik Impas)
- Menghitung jumlah unit yang perlu dijual untuk menutupi biaya produksi.
- Memprediksi profitabilitas suatu usaha.
Studi Kasus
Misalnya, dalam studi kasus perusahaan manufaktur, penyelesaian persamaan digunakan untuk menentukan jumlah unit yang perlu diproduksi untuk memaksimalkan laba. Dengan menyelesaikan persamaan pendapatan sama dengan biaya, perusahaan dapat menemukan titik impas dan membuat keputusan produksi yang tepat.
Tips dan Trik

Untuk mempercepat penyelesaian persamaan, terdapat beberapa tips dan trik yang dapat diterapkan. Dengan mengidentifikasi jenis persamaan yang dapat diselesaikan secara mental atau menggunakan alat bantu, serta menerapkan strategi yang tepat, proses penyelesaian persamaan dapat menjadi lebih efisien dan efektif.
Menentukan selesaian dari persamaan berikut memerlukan pemahaman yang cermat terhadap simbol-simbol matematika. Sama pentingnya untuk memperhatikan simbol simbol keselamatan di laboratorium saat melakukan eksperimen yang melibatkan bahan kimia atau peralatan berbahaya. Simbol-simbol ini memberikan peringatan visual yang jelas tentang potensi bahaya, memungkinkan peneliti untuk mengambil tindakan pencegahan yang tepat dan memastikan keselamatan selama bekerja di lingkungan laboratorium.
Memahami simbol-simbol keselamatan ini tidak hanya melengkapi pengetahuan matematika tetapi juga berkontribusi pada praktik laboratorium yang aman, yang sangat penting untuk menentukan selesaian persamaan secara akurat dan andal.
Mengidentifikasi Persamaan yang Dapat Diselesaikan Secara Mental
Beberapa persamaan sederhana dapat diselesaikan secara mental tanpa menggunakan alat bantu. Persamaan ini biasanya melibatkan operasi dasar seperti penjumlahan, pengurangan, perkalian, atau pembagian bilangan kecil. Misalnya, persamaan seperti 5 + 3 atau 10 – 2 dapat diselesaikan dengan cepat dalam pikiran.
Menggunakan Kalkulator atau Perangkat Lunak Matematika, Tentukan selesaian dari persamaan berikut
Untuk persamaan yang lebih kompleks, kalkulator atau perangkat lunak matematika dapat sangat membantu. Alat bantu ini dapat melakukan perhitungan yang memakan waktu atau rumit dengan cepat dan akurat, membebaskan waktu untuk fokus pada pemahaman konseptual persamaan.
Strategi untuk Persamaan yang Menantang
Persamaan yang lebih menantang atau kompleks mungkin memerlukan strategi khusus untuk diselesaikan. Salah satu strategi adalah memecah persamaan menjadi beberapa langkah yang lebih kecil dan mudah dikelola. Strategi lain melibatkan penggunaan sifat-sifat operasi matematika, seperti sifat distributif atau sifat asosiatif, untuk menyederhanakan persamaan dan membuatnya lebih mudah untuk diselesaikan.
Pemungkas

Menguasai teknik penyelesaian persamaan tidak hanya meningkatkan kemampuan matematika Anda, tetapi juga membekali Anda dengan alat yang berharga untuk memecahkan masalah di berbagai disiplin ilmu.
FAQ Terpadu
Apa itu persamaan matematika?
Persamaan matematika adalah pernyataan yang menyatakan bahwa dua ekspresi matematika memiliki nilai yang sama.
Mengapa penting untuk menyelesaikan persamaan?
Penyelesaian persamaan sangat penting untuk memecahkan masalah dalam berbagai bidang, seperti fisika, kimia, dan ekonomi.
Apa saja jenis-jenis persamaan umum?
Jenis persamaan umum meliputi persamaan linear, kuadrat, dan kubik.
Apa saja metode umum untuk menyelesaikan persamaan?
Metode umum untuk menyelesaikan persamaan meliputi faktorisasi, melengkapi kuadrat, dan rumus kuadrat.