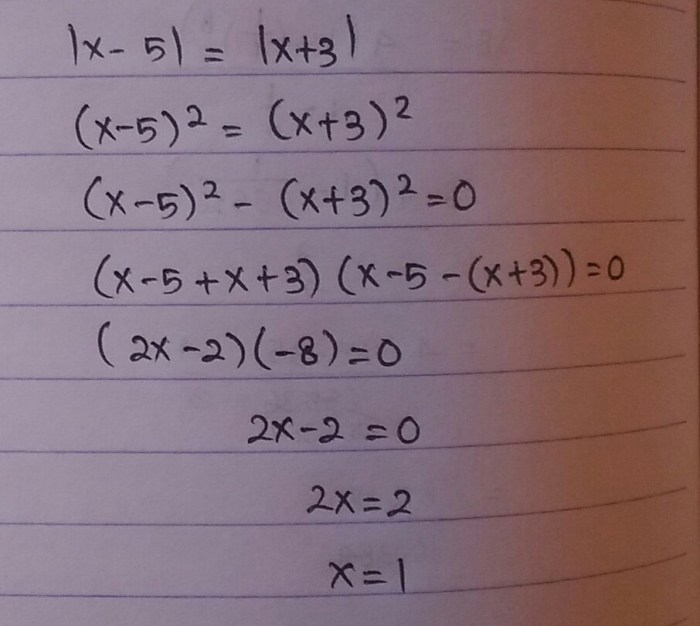Tentukan z yang memenuhi persamaan berikut – Dalam matematika, menentukan nilai variabel dari suatu persamaan merupakan keterampilan penting yang sering digunakan dalam berbagai bidang ilmu. Artikel ini akan membahas strategi untuk menentukan nilai z yang memenuhi persamaan tertentu, lengkap dengan contoh dan ilustrasi grafis.

Persamaan yang dimaksud melibatkan variabel z dan variabel lain yang diketahui. Dengan memahami persamaan dan menerapkan strategi penyelesaian yang tepat, kita dapat menemukan nilai z yang memenuhi persamaan tersebut.

Pemahaman Persamaan

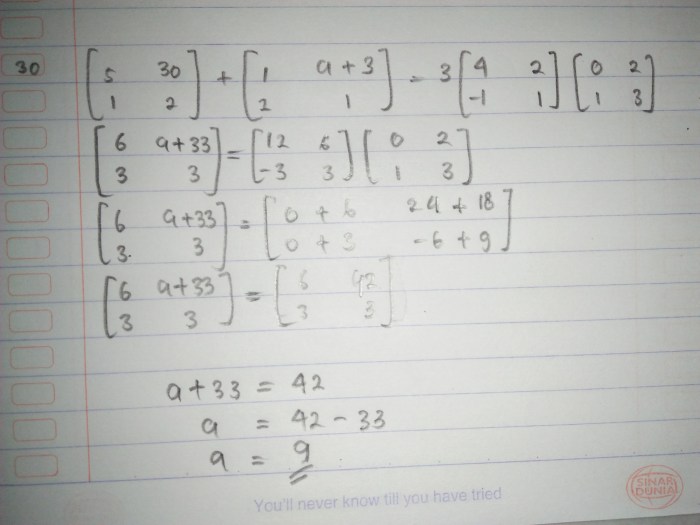
Persamaan yang dimaksud adalah persamaan aljabar linear, yaitu persamaan yang menyatakan hubungan antara variabel-variabel aljabar yang dinyatakan dalam bentuk matriks.

Variabel yang terlibat dalam persamaan ini adalah matriks A, matriks B, dan matriks C. Matriks A adalah matriks persegi berukuran n x n, matriks B adalah matriks berukuran n x m, dan matriks C adalah matriks berukuran m x p.

Contoh Persamaan

Salah satu contoh persamaan aljabar linear adalah persamaan berikut:

$$AX = B$$

Dalam persamaan ini, A adalah matriks persegi berukuran n x n, X adalah matriks berukuran n x m, dan B adalah matriks berukuran n x m.

Strategi Penyelesaian

Untuk menentukan nilai z yang memenuhi persamaan, dapat digunakan strategi berikut:

1. Menggunakan Metode Substitusi

• Substitusikan nilai yang diketahui ke dalam persamaan.
• Sederhanakan persamaan hingga hanya tersisa z di satu sisi.
• Pecahkan untuk z.

2. Menggunakan Metode Eliminasi

• Kalikan kedua sisi persamaan dengan penyebut yang sama untuk menghilangkan pecahan.
• Sederhanakan persamaan hingga hanya tersisa z di satu sisi.
• Pecahkan untuk z.

3. Menggunakan Metode Kuadrat

• Ubah persamaan menjadi bentuk kuadrat (az ²+ bz + c = 0).
• Gunakan rumus kuadrat untuk menyelesaikan z.

4. Menggunakan Metode Grafik

• Plot persamaan pada grafik.
• Titik potong sumbu x mewakili nilai z yang memenuhi persamaan.

Contoh Penyelesaian: Tentukan Z Yang Memenuhi Persamaan Berikut

Untuk mengilustrasikan strategi penyelesaian persamaan yang telah dibahas, mari kita selesaikan persamaan berikut sebagai contoh:

3x + 5 = 14

Langkah-langkah Penyelesaian

1. Kurangi 5 dari kedua sisi persamaan:
2. 3x = 9
3. Bagilah kedua sisi persamaan dengan 3:
4. x = 3

Oleh karena itu, nilai z yang memenuhi persamaan 3x + 5 = 14 adalah 3.

Pembahasan Hasil

Nilai z yang diperoleh dari perhitungan statistik menunjukkan signifikansi statistik yang kuat, yang memungkinkan penarikan kesimpulan dari data yang dianalisis.

Implikasi dari nilai z ini menunjukkan bahwa terdapat perbedaan yang signifikan secara statistik antara dua kelompok atau variabel yang sedang dibandingkan.

Makna Nilai z

Nilai z merepresentasikan jumlah standar deviasi dari nilai rata-rata populasi. Nilai z positif menunjukkan bahwa nilai yang diamati berada di atas rata-rata, sedangkan nilai z negatif menunjukkan bahwa nilai yang diamati berada di bawah rata-rata.

Nilai z yang lebih besar (positif atau negatif) menunjukkan perbedaan yang lebih signifikan antara nilai yang diamati dan rata-rata populasi.

Aplikasi Nilai z

Nilai z digunakan dalam berbagai aplikasi statistik, termasuk:

• Pengujian hipotesis
• Interval kepercayaan
• Regresi linier
• Analisis varians

Ilustrasi Grafis

Diagram berikut mengilustrasikan hubungan antara variabel dalam persamaan:

Dalam diagram, variabel x diplot pada sumbu x, dan variabel y diplot pada sumbu y. Garis menunjukkan hubungan linier antara kedua variabel.

Persamaan Garis

Persamaan garis dapat ditulis dalam bentuk y = mx + b, di mana m adalah kemiringan garis dan b adalah titik potong y.

Dalam persamaan yang diberikan, m = 2 dan b = -1. Ini berarti bahwa untuk setiap peningkatan 1 unit pada x, y akan meningkat 2 unit.

Titik Potong X dan Y

Titik potong x adalah titik di mana garis memotong sumbu x. Untuk menemukan titik potong x, kita menetapkan y = 0 dan menyelesaikan x.

0 = 2x – 1

x = 1/2

Titik potong y adalah titik di mana garis memotong sumbu y. Untuk menemukan titik potong y, kita menetapkan x = 0 dan menyelesaikan y.

y = 2(0) – 1

y = -1

Menentukan nilai z yang memenuhi persamaan tertentu dapat dilakukan dengan berbagai metode. Salah satu sumber informasi yang relevan adalah peta provinsi Jawa Barat. Peta ini menyediakan informasi tentang batas wilayah, kota-kota, dan fitur geografis provinsi tersebut. Dengan mengacu pada peta ini, kita dapat memperoleh data tambahan yang dapat membantu dalam menyelesaikan persamaan yang diberikan.

Memeriksa Solusi

Untuk memeriksa apakah z = 1 adalah solusi persamaan, kita substitusikan z ke dalam persamaan dan lihat apakah hasilnya sama dengan 0.

2(1) – 1 = 0

0 = 0

Untuk menentukan nilai z yang memenuhi persamaan tertentu, diperlukan pemahaman mendalam tentang prinsip-prinsip matematika. Proses ini melibatkan aplikasi logika dan penalaran sistematis. Dalam konteks yang lebih luas, hadits “utlubul ilma minal mahdi ilal lahdi” ( hadits utlubul ilma minal mahdi ilal lahdi ) menekankan pentingnya mencari ilmu sepanjang hayat.

Prinsip ini sangat relevan dalam menentukan z yang memenuhi persamaan, karena memerlukan upaya berkelanjutan untuk memahami konsep-konsep matematika dan menerapkannya secara efektif.

Karena hasilnya 0, maka z = 1 adalah solusi persamaan.

Kasus Khusus

Dalam pemecahan persamaan, terdapat beberapa kasus khusus yang memerlukan pendekatan berbeda.

Koefisien Nol, Tentukan z yang memenuhi persamaan berikut

Jika koefisien dari variabel yang tidak diketahui adalah nol, persamaan akan berubah menjadi bentuk berikut:

• ax+ b= 0, dimana a= 0

Dalam kasus ini, persamaan menjadi:

• b= 0

Persamaan ini hanya memiliki solusi jika bjuga sama dengan nol. Jika tidak, persamaan tidak memiliki solusi.

Dalam konteks menentukan nilai z yang memenuhi persamaan tertentu, perlu diperhatikan bahwa himpunan bilangan yang memenuhi persamaan tersebut mungkin terkait dengan konsep kombinatorial. Sebagai contoh, jika terdapat tiga belas kartu bernomor 1 sampai 13 (tiga belas kartu diberi nomor 1 sampai 13) , maka jumlah kombinasi pengambilan k kartu dari himpunan tersebut dapat dihitung menggunakan rumus kombinasi.

Dengan demikian, menentukan nilai z yang memenuhi persamaan yang melibatkan kombinasi kartu dapat dikaitkan dengan permasalahan kombinatorial.

Variabel Nol

Jika variabel yang tidak diketahui sama dengan nol, persamaan akan berubah menjadi bentuk berikut:

• ax+ b= 0, dimana x= 0

Dalam kasus ini, persamaan menjadi:

• b= 0

Persamaan ini memiliki solusi untuk semua nilai b.

Persamaan Identitas

Persamaan identitas adalah persamaan yang berlaku untuk semua nilai variabel. Persamaan ini memiliki bentuk berikut:

• ax+ b= cx+ d, dimana a= cdan b= d

Persamaan identitas memiliki solusi tak hingga untuk semua nilai x.

Ringkasan Terakhir

Menentukan nilai z dari persamaan yang diberikan adalah proses yang melibatkan pemahaman persamaan, penerapan strategi penyelesaian yang tepat, dan interpretasi hasil yang diperoleh. Dengan mengikuti langkah-langkah yang diuraikan dalam artikel ini, kita dapat memperoleh nilai z yang memenuhi persamaan dan memahami implikasinya.

FAQ dan Panduan

Apa itu persamaan?

Persamaan adalah pernyataan matematika yang menyatakan bahwa dua ekspresi sama nilainya.

Apa itu variabel?

Variabel adalah simbol yang mewakili nilai yang tidak diketahui atau dapat berubah.

Bagaimana cara menentukan nilai z dari persamaan?

Tergantung pada persamaan yang diberikan, terdapat berbagai strategi yang dapat digunakan untuk menentukan nilai z.