Dalam dunia geometri, konsep persamaan garis dan titik koordinat memainkan peran penting dalam menentukan hubungan antara titik-titik pada bidang. Tulisan ini akan membahas cara menentukan apakah tiga atau empat titik dilalui oleh persamaan garis yang sama, memberikan wawasan tentang sifat-sifat geometris yang mendasarinya.
Persamaan garis mendefinisikan suatu garis lurus pada bidang koordinat Cartesius. Persamaan garis tersebut dinyatakan dalam bentuk y = mx + c, di mana m adalah kemiringan garis dan c adalah titik potong y. Dengan memahami persamaan garis, kita dapat mengidentifikasi titik-titik yang terletak pada garis tersebut.
Persamaan Garis
Persamaan garis adalah representasi matematis dari sebuah garis yang menghubungkan dua titik atau lebih pada bidang koordinat. Persamaan ini menggambarkan hubungan antara koordinat x dan y dari titik-titik yang terletak pada garis tersebut.
Rumus umum persamaan garis adalah y = mx + b, di mana:
- y adalah koordinat y titik pada garis
- x adalah koordinat x titik pada garis
- m adalah kemiringan garis (perubahan y dibagi dengan perubahan x)
- b adalah titik potong y (nilai y saat x = 0)
Sebagai contoh, persamaan garis y = 2x + 1 mewakili garis dengan kemiringan 2 dan titik potong y 1.
Titik Koordinat
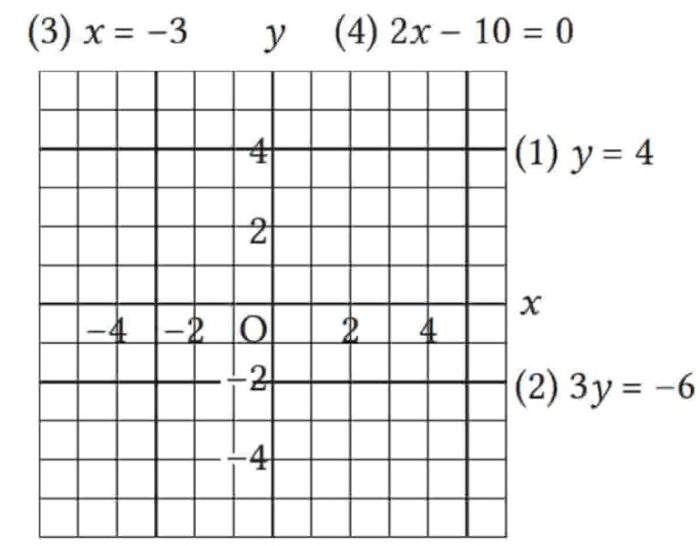
Dalam matematika, titik koordinat adalah sebuah lokasi pada bidang dua dimensi yang ditentukan oleh sepasang angka, yang disebut koordinat. Koordinat ini mewakili jarak titik dari dua sumbu tegak lurus, yang disebut sumbu x dan sumbu y.
Untuk menentukan koordinat suatu titik pada bidang Cartesius, kita mengukur jarak titik tersebut dari titik asal (0, 0) di sepanjang sumbu x dan sumbu y. Koordinat titik ditulis dalam bentuk (x, y), di mana x adalah koordinat x dan y adalah koordinat y.
Contoh Titik Koordinat
- (2, 3) adalah titik yang terletak 2 satuan ke kanan dari titik asal dan 3 satuan ke atas.
- (-1, 5) adalah titik yang terletak 1 satuan ke kiri dari titik asal dan 5 satuan ke atas.
- (0, 0) adalah titik asal, yang terletak pada perpotongan sumbu x dan sumbu y.
Titik pada Persamaan Garis

Persamaan garis adalah persamaan matematika yang menggambarkan sebuah garis lurus pada bidang koordinat. Persamaan ini memungkinkan kita menentukan apakah sebuah titik terletak pada garis tersebut atau tidak.
Untuk menentukan apakah sebuah titik terletak pada persamaan garis, kita dapat mensubstitusikan koordinat titik tersebut ke dalam persamaan garis. Jika hasil substitusi tersebut menghasilkan nilai 0, maka titik tersebut terletak pada garis.
Titik pada Persamaan Garis y = 2x + 1
| x | y |
|---|---|
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
Tiga dan Empat Titik
Dalam geometri, menentukan apakah titik-titik terletak pada garis atau bidang yang sama merupakan tugas penting. Berikut adalah langkah-langkah untuk menentukan apakah tiga titik berada pada garis yang sama dan apakah empat titik berada pada bidang yang sama.
Tiga Titik pada Garis yang Sama
- Tentukan persamaan garis yang melalui dua titik dari tiga titik yang diberikan.
- Ganti koordinat titik ketiga ke dalam persamaan garis.
- Jika titik ketiga memenuhi persamaan garis, maka ketiga titik tersebut terletak pada garis yang sama.
Empat Titik pada Bidang yang Sama
- Tentukan persamaan bidang yang melalui tiga titik dari empat titik yang diberikan.
- Ganti koordinat titik keempat ke dalam persamaan bidang.
- Jika titik keempat memenuhi persamaan bidang, maka keempat titik tersebut terletak pada bidang yang sama.
Ilustrasi Grafis

Ilustrasi grafis dapat memberikan gambaran visual tentang konsep matematika. Dua ilustrasi berikut menunjukkan titik-titik yang terletak pada garis dan bidang.
Tiga Titik pada Garis
Titik-titik yang terletak pada garis yang sama disebut titik kolinear. Ilustrasi berikut menunjukkan tiga titik A, B, dan C yang terletak pada garis l.

Empat Titik pada Bidang
Titik-titik yang terletak pada bidang yang sama disebut titik koplanar. Ilustrasi berikut menunjukkan empat titik A, B, C, dan D yang terletak pada bidang P.

Ringkasan Penutup

Secara keseluruhan, analisis apakah tiga atau empat titik dilalui oleh persamaan garis yang sama memberikan pemahaman mendalam tentang hubungan geometris antara titik-titik tersebut. Melalui pemahaman konsep ini, kita dapat memecahkan berbagai masalah geometri dan memperoleh wawasan tentang sifat-sifat dasar garis dan titik pada bidang koordinat.
Ringkasan FAQ
Apa saja langkah-langkah untuk menentukan apakah tiga titik dilalui oleh garis yang sama?
Tentukan persamaan garis yang melalui dua titik pertama. Periksa apakah titik ketiga terletak pada garis tersebut dengan mensubstitusikan koordinatnya ke dalam persamaan.
Bagaimana cara menentukan apakah empat titik dilalui oleh bidang yang sama?
Tentukan persamaan garis yang melalui tiga titik pertama. Periksa apakah titik keempat terletak pada garis tersebut dengan mensubstitusikan koordinatnya ke dalam persamaan. Jika tidak terletak pada garis tersebut, maka keempat titik tidak dilalui oleh bidang yang sama.
